
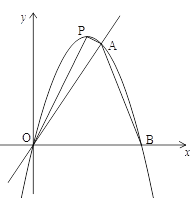
【题目】如图,抛物线y=ax2+bx的顶点为P(2,4),直线y=![]() x与抛物线交于点A.抛物线与x轴的另一个交点是点B.
x与抛物线交于点A.抛物线与x轴的另一个交点是点B.
(1)求抛物线的解析式和点A的坐标;
(2)求四边形APOB的面积;
(3)M是抛物线上位于直线y=![]() x上方的一点,当点M的坐标为多少时,△MOA的面积最大?
x上方的一点,当点M的坐标为多少时,△MOA的面积最大?
【答案】(1)y=-x2+4x,A(![]() ,
,![]() );(2)
);(2)![]() ;(3)M(
;(3)M(![]() ,
,![]() ).
).
【解析】
(1)因为顶点为P(2,4),所以带入顶点坐标公式就可以求得解析式;抛物线的解析式和直线解析式联立组成方程组,即可求出点A的坐标;
(2)把四边形APOB的面积分割成两个直角三角形和直角梯形;
(3)作MN∥y轴,交OA于点N,设M(m,-m2+4m),则N(m,![]() m),所以MN=-m2+4m-
m),所以MN=-m2+4m-![]() m=-m2+
m=-m2+![]() m,可得:S△MOA=
m,可得:S△MOA=![]() ×
×![]() ×(-m2+
×(-m2+![]() m)=-
m)=-![]() m2+
m2+![]() m,根据抛物线开口向下,所以面积有最大值得解.
m,根据抛物线开口向下,所以面积有最大值得解.
解:(1)由题意得: ,解得
,解得![]()
∴y=-x2+4x
∵直线y=![]() x与抛物线交于点A ,
x与抛物线交于点A ,
∴ 解得
解得![]() ,
, ,即A(
,即A(![]() ,
,![]() )
)
(2)∵y=-x2+4x与x轴的另一个交点是点B.
∴y=0代入解析式得:-x2+4x=0,
解得x1=0 , x2=4,∴点B的坐标是(4,0)
∴S四边形APOB=![]() ×2×4+
×2×4+![]() (4+
(4+![]() )×(
)×(![]() -2)+
-2)+![]() ×(4-
×(4-![]() )×
)×![]() =
=![]()
(3)如图,作MN∥y轴,交OA于点N,设M(m,-m2+4m),则N(m,![]() m)
m)
∴MN=-m2+4m-![]() m=-m2+
m=-m2+![]() m
m
∴S△MOA=![]() ×
×![]() ×(-m2+
×(-m2+![]() m)=-
m)=-![]() m2+
m2+![]() m.
m.
∵-![]() <0,开口向下,
<0,开口向下,
∴当m= -![]() =
= ![]() 时,S△MOA最大,
时,S△MOA最大,
即M(![]() ,
,![]() )
)



 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
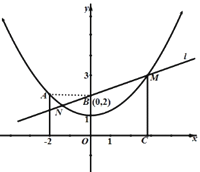
【题目】如图,已知二次函数y=ax2+1(a≠0,a为实数)的图象过点A(-2,2),一次函数y=kx+b(k≠0,k、b为实数)的图象l经过点B(0,2).
(1)求a的值并写出二次函数表达式;
(2)求b的值;
(3)设直线l与二次函数图象交于M、N两点,过M作MC垂直x轴于点C,试证明:MB=MC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=60°,∠BEQ=45°;在点F处测得∠AFP=45°,∠BFQ=90°,EF=2km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
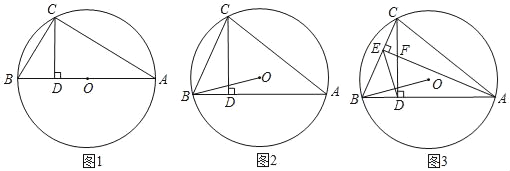
【题目】如图所示,![]() 内接于圆O,
内接于圆O,![]() 于D;
于D;
(1)如图1,当AB为直径,求证:![]() ;
;
(2)如图2,当AB为非直径的弦,连接OB,则(1)的结论是否成立?若成立请证明,不成立说明由;
(3)如图3,在(2)的条件下,作![]() 于E,交CD于点F,连接ED,且
于E,交CD于点F,连接ED,且![]() ,若
,若![]() ,
,![]() ,求CF的长度.
,求CF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆锥的底面半径为10 cm,高为10![]() cm.
cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥侧面一周回到SA上的点M处,且SM=3AM,求它所走的最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A,B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°.
(1)求线段AB的长;
(2)求经过A,B两点的反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
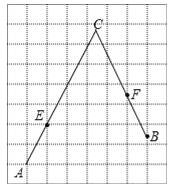
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(Ⅰ)AE的长等于 ;
(Ⅱ)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
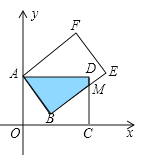
(1)求AD的长;
(2)求阴影部分的面积和直线AM的解析式;
(3)求经过A、B、D三点的抛物线的解析式;
(4)在抛物线上是否存在点P,使![]() ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:
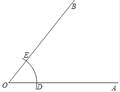
已知:∠AOB.
求作:射线OC,使它平分∠AOB.
作法:
(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
(2)分别以D、E为圆心,大于![]() DE的同样长为半径作弧,两弧相交于点C;
DE的同样长为半径作弧,两弧相交于点C;
(3)作射线OC.
所以射线OC就是所求作的射线.
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连结CE,CD.
∵OE=OD, = ,OC=OC,
∴△OEC≌△ODC(依据: ),
∴∠EOC=∠DOC,
即OC平分∠AOB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com