
����Ŀ������ʦ��ѧ������һ���⣺
��(2a+b)(2a��b)+2(2a��b)2+(2ab2��16a2b)��(��2a)��ֵ������a��![]() ��b����1��ͬѧ�ǿ�����Ŀ����ͬ�Ŀ�����С��˵������b����1�Ƕ���ģ���С��˵������������������Ͳ��������������Բ����࣮��
��b����1��ͬѧ�ǿ�����Ŀ����ͬ�Ŀ�����С��˵������b����1�Ƕ���ģ���С��˵������������������Ͳ��������������Բ����࣮��
(1)����Ϊ����˭˵���е�����Ϊʲô��
(2)��xm���ڱ��}����Ľ��������x2m��ֵ��
���𰸡�(1)С��˵���е��������ɼ�������(2)9.
��������
��1���ԣ�2a+b����2a-b��+2��2a-b��2+��2ab2-16a2b������-2a��ͨ��������������л���
��2���ɣ�1���ɼ���õĽ��Ϊ3����xm=3����x2m=��xm��2=32=9.
��1��С��˵���е������������£�
(2a+b)(2a��b)+2(2a��b)2+(2ab2��16a2b)��(��2a)
��(2a)2��b2+2(4a2��4ab+b2)+(��2b+8ab)
��4a2��b2+8a2��8ab+2b2��b2+8ab
��12a2
����Ľ��Ϊ12a2������ĸb��
������b����1�Ƕ���ģ�С��˵���е�����
��2����a��![]() ʱ��12a2��12��(
ʱ��12a2��12��(![]() )2��3��
)2��3��
������֪xm��3��
��x2m��(xm)2��32��9��
��x2m��ֵΪ9


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y��x�뷴��������y��![]() ��x��0��ͼ����A������A��AC��x�ᣬ����ΪC��һ�κ���y��kx+b��ͼ����A����y��������ύ��B��
��x��0��ͼ����A������A��AC��x�ᣬ����ΪC��һ�κ���y��kx+b��ͼ����A����y��������ύ��B��
��1�����A�����ꣻ
��2�����ı���ABOC�����Ϊ3����һ�κ���y��kx+b�ı���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB=90�㣬AC=8��BC=6����D���Ե�AΪԲ��4Ϊ�뾶��Բ��һ�㣬����BD����MΪBD�е㣬�߶�CM���ȵ����ֵΪ �� 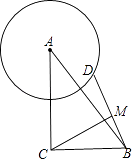
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬��D��AB���е㣬��E��BC����һ�㣬����ADE��DE�۵����õ���FDE��ʹ��FDE���BDE�ص����ֵ�����ǡ�AEB�����![]() ����AC��3��BC��6�����߶�BE�ij�Ϊ__________��
����AC��3��BC��6�����߶�BE�ij�Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD����E��CD�ϣ�����AE��BD����G��AE�е㣬����G��FH��AE��FH�ֱ�AD��BC�ڵ�F��H��FH��BD���ڵ�K����HK��2FG����EG��![]() �����߶�AF�ij�Ϊ_______________��
�����߶�AF�ij�Ϊ_______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˻��̵��������ס�������������ۣ�ÿ����������Ľ��۱�ÿ����������Ľ��۶�20Ԫ������3����������ķ��ú���4����������ķ�����ȣ��ּƻ��������������100���������������������35����
��1�������������Ϊ__________Ԫ/���������������Ϊ__________Ԫ/����
��2�����������ÿ���ۼ�120Ԫ���������ÿ���ۼ�90Ԫ���ҹ�����100������ķ��ò�����7200Ԫ�������100������������꣬��ô�˻��̵���ν������ܻ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У���A��100������C��70������M��N�ֱ���AB��BC�ϣ�����BMN��MN���ۣ�����FMN����MF��AD��FN��DC�����D��_____����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC �У�AB=AC����B=50�㣬P �DZ� AB �ϵ�һ������(���붥�� A �غ�)������BPC �Ķ���������

A. 50�� B. 80�� C. 100�� D. 130��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������������࣬С��д��һ�Ⳬ���飬����ת���ķ�ʽ����������������µ�ת�����������鷢�����Լ������ϣ�Ȼ������![]() ������ת����ÿ������ת��֮��������
������ת����ÿ������ת��֮��������![]() ��������ͬ�ĺ���ת������֪��������ת������
��������ͬ�ĺ���ת������֪��������ת������![]() �� �˲����˱��λ��
�� �˲����˱��λ��
��1��x��ֵ�Ƕ��٣�
��2���پ�������ת�����������ᳬ��![]() �ˣ�
�ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com