
 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
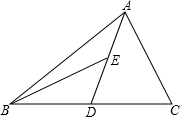 如图,AD为△ABC的中线,BE为△ABD中线
如图,AD为△ABC的中线,BE为△ABD中线查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某服装网店李经理用11000元购进了甲、乙两种款式的童装共150件,两种童装的价格如右图所示,请你求出李经理购买甲乙两种款式的童装各多少件?
某服装网店李经理用11000元购进了甲、乙两种款式的童装共150件,两种童装的价格如右图所示,请你求出李经理购买甲乙两种款式的童装各多少件?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com