
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,连结AE、DE、DC,且AE=CD.

(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AC=BC,∠C=120°,点D为AB边的中点,∠EDF=60°,DE、DF分别交AC、BC与E、F点。
(1)如图,若EF∥AB,求证DE=DF
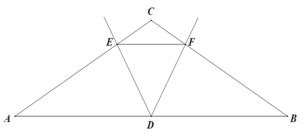
(2)如图,若EF与AB不平行,则问题(1)的结论是否成立?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
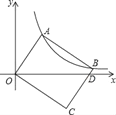
【题目】如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=![]() ( x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为( )
( x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为( )
A. (3,![]() ) B. (4,
) B. (4,![]() ) C. (
) C. (![]() ,
,![]() ) D. (5,
) D. (5,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )
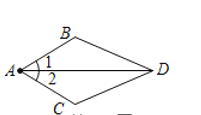
A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
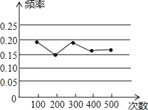
A. 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”
B. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
C. 掷一枚质地均匀的硬币,落地时结果是“正面朝上”
D. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
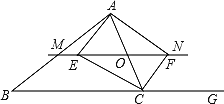
【题目】已知:如图,△ABC中,点O是AC上的一动点,过点O作直线MN∥AB,设MN交∠BCA的平分线于点E,交∠BCA的外角∠ACG的平分线于点F连接AE、AF.
(1)求证:∠ECF=90°;
(2)当点O运动到何处时,四边形AECF是矩形?请说明理由;
(3)在(2)的条件下,△ABC应该满足条件:______________,就能使矩形AECF变为正方形。(直接添加条件,无需证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com