
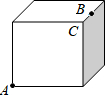
 在正方体的一个顶点A处有一只蚂蚁,现在要向点B处爬行,已知正方体的棱长为3cm,BC=1cm,则爬行的最短距离是多少?
在正方体的一个顶点A处有一只蚂蚁,现在要向点B处爬行,已知正方体的棱长为3cm,BC=1cm,则爬行的最短距离是多少?  星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:选择题
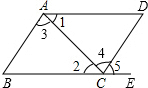 如图,给出下列条件:①∠3=∠4;②∠1=∠2;③∠5=∠B;④AD∥BE,且∠D=∠B;⑤∠1+∠3+∠B=180°.其中能说明AB∥DC的条件有( )
如图,给出下列条件:①∠3=∠4;②∠1=∠2;③∠5=∠B;④AD∥BE,且∠D=∠B;⑤∠1+∠3+∠B=180°.其中能说明AB∥DC的条件有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
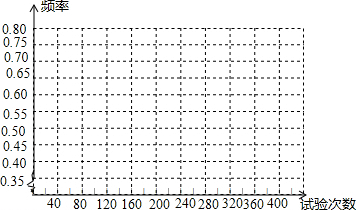
| 试验次数 | 20 | 80 | 100 | 160 | 200 | 240 | 300 | 360 | 400 |
| “车”字朝上的频数 | 14 | 48 | 50 | 84 | 112 | 144 | 172 | 204 | 228 |
| 相应的频率 | 0.70 | 0.60 | 0.50 | 0.53 | 0.56 | 0.60 | 0.57 | 0.57 | 0.57 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)请在如图的网格中建立适当的平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,-2);
(1)请在如图的网格中建立适当的平面直角坐标系,使得A,B两点的坐标分别为(4,1),(1,-2);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com