
如图,在 中,
中, 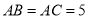 ,
,  ,点
,点 是
是 上的动点,过点
上的动点,过点 作
作 于点
于点 ,
,  于点
于点 ,则
,则 __________.
__________.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年七年级上学期期终模拟数学试卷 题型:解答题
如图1,已知数轴上两点A、B对应的数分别为﹣2、5,点P为数轴上的一动点,其对应的数为x.

(1)PA= ;PB= (用含x的式子表示)
(2)在数轴上是否存在点P,使PA+PB=10?若存在,请直接写出x的值;若不存在,请说明理由.
(3)如图2,点P以2个单位/s的速度从点O向右运动,同时点A以4个单位/s的速度向左运动,点B以16个单位/s的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问: 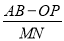 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源:浙江杭州余杭区2016-2017学年八年级上学期期末数学试卷 题型:解答题
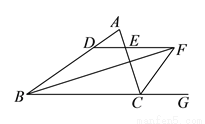
如图,在 中,
中,  ,
,  的平分线
的平分线 与
与 的外角平分线交于点
的外角平分线交于点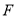 ,过点
,过点 作
作 ,交
,交 于点
于点 ,交
,交 于点
于点 .
.
( )图中除
)图中除 之外,还有几个等腰三角形,请分别写出来;
之外,还有几个等腰三角形,请分别写出来;
( )若
)若 ,
,  ,求
,求 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州余杭区2016-2017学年八年级上学期期末数学试卷 题型:单选题
证明命题“任何偶数都是 的整数倍”是假命题,下列各数可以作为反例的是( ).
的整数倍”是假命题,下列各数可以作为反例的是( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:解答题
如图,在 中,
中,  平分
平分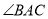 ,且
,且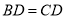 ,
,  于点
于点 ,
,  于点
于点 .
.

( )求证:
)求证: 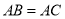 .
.
( )若
)若 ,
, 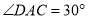 ,求
,求 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:单选题
有一个边长为 的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图
的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图 ),且三个正方形所围成的三角形是直角三角形;再经过一次“生长’’后变成了图
),且三个正方形所围成的三角形是直角三角形;再经过一次“生长’’后变成了图 ,如此继续“生长”下去,则“生长”第七次后所有正方形的面积和为( ).
,如此继续“生长”下去,则“生长”第七次后所有正方形的面积和为( ).


A. 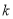 B.
B.  C.
C. 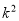 D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:单选题
下列命题是假命题的是( )
A. 有一个角为 的等腰三角形是等边三角形
的等腰三角形是等边三角形
B. 等角的余角相等
C. 钝角三角形一定有一个角大于
D. 同位角相等
D 【解析】选项A、B、C都是真命题;选项D,两直线平行,同位角相等,选项D错误,是假命题,故选D.查看答案和解析>>
科目:初中数学 来源:人教版2017-2018学年七年级下册5.2《平行线的判定》检测数学试卷 题型:解答题
如图,已知∠ABC=∠ACB,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由.

查看答案和解析>>
科目:初中数学 来源:安徽省太和县2017-2018学年度第一学期期末考试七年级数学试卷 题型:解答题
一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了3小时.已知水流的速度是3千米/时,求船在静水中的平均速度.
静水平均速度15千米/时. 【解析】等量关系为:顺水速度×顺水时间=逆水速度×逆水时间.即:2×(静水速度+水流速度)=2.5×(静水速度-水流速度).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com