
分析 (1)先设y=x2+x,则原方程变形为y2+2y-8=0,运用因式分解法解得y1=-4,y2=2,再把y=-4和2分别代入y=x2+x得到关于x的一元二次方程,然后解两个一元二次方程,最后确定原方程的解;
(2)首先设x=a+b,求得方程x2-7x+10=0的解,得出a+b的数值,根据勾股定理可得a2+b2=c2,再利用完全平方公式整理得到ab,然后根据三角形的面积公式求解即可.
解答 解:(1)设y=x2+x,
原方程变形为y2+2y-8=0,
(y+4)(y-2)=0,
解得y1=-4,y2=2,
当y=-4时,x2+x=-4,x2+x+4=0,△=1-4×4<0,此方程无实数解;
当y=2时,x2+x=2,x2+x-2=0,解得x1=-2,x2=1,
所以原方程的解为x1=-2,x2=1.
(2)设x=a+b,则原方程为x2-7x+10=0,
解得:x=2或x=5,
即a+b=2,a+b=5,由斜边c=4,舍去a+b=2,
Rt△ABC的周长为4+5=9;
由勾股定理得a2+b2=42,
则(a+b)2-2ab=16
解得:ab=$\frac{9}{2}$,
因此Rt△ABC的面积=$\frac{1}{2}$ab=$\frac{9}{4}$.
点评 本题考查了换元法解一元二次方程,勾股定理的运用.我们常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解某班学生“50米跑”的成绩 | |
| B. | 了解一批袋装食品是否含有防腐剂 | |
| C. | 了解江苏卫视“非诚勿扰”节目的收视率 | |
| D. | 了解一批灯泡的使用寿命 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
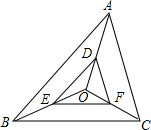 如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC.
如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com