
����Ŀ��ij��˾����Ƹһ��Ա������ӦƸ�ס��ҡ����ӱ��ԡ����ԡ�����������������������ˣ��ס��ҡ�������÷����±���
�� �� | �� �� | �� �� | |
�� | 85 | 80 | 75 |
�� | 80 | 90 | 73 |
�� | 83 | 79 | 90 |
��1����������÷ֵ�ƽ���֣��Ӹߵ���ȷ������ӦƸ�ߵ�����˳��
��2���ù�˾�涨�����ԣ����ԡ����ܵ÷ֱַõ���80�֣�80�֣�70�֣�����60%��30%��10%�ı��������ܷ֣�������������������������˵��˭����¼�ã�
���𰸡���1�������ң��ף���2���ױ�¼�ã�
��������
��1��������ƽ������ʽ����������˵�ƽ���ɼ����Ƚϵó������
��2��������ס��ҡ������ܷ֣����ݹ�˾�Ĺ涨���ų������ٸ��ݼ��ܷ���ߣ����ɵó��ױ�¼�ã�
��1��![]() ��=��85+80+75����3=80���֣���
��=��85+80+75����3=80���֣���![]() ��=��80+90+73����3=81���֣���
��=��80+90+73����3=81���֣���![]() ��=��83+79+90����3=84���֣�����Ӹߵ���ȷ������ӦƸ�ߵ�����˳��Ϊ�������ң��ף�
��=��83+79+90����3=84���֣�����Ӹߵ���ȷ������ӦƸ�ߵ�����˳��Ϊ�������ң��ף�
��2�����ܷ�����85��60%+80��30%+75��10%=82.5���֣����ҵ��ܷ�����80��60%+90��30%+73��10%=82.3���֣��������ܷ�����83��60%+79��30%+90��10%=82.5���֣���
�߹�˾�涨�����������ԡ����ܵ÷ֱַõ���80����80����70��������ų�������ܷ�������ױ�¼�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ίԱͳ����ȫ��45��ͬѧһ�ܵ���������ʱ�䣨��λ��Сʱ��������������ͼ��ʾ������ͳ��ͼ������˵���д�����ǣ� ��

A. ����ʱ����9Сʱ��������� B. ����ʱ����10Сʱ����10��
C. ����ʱ����11Сʱ����4�� D. ����ʱ�䲻����9Сʱ����14��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2��ͼ����һ�κ���y=x+b��ͼ���ཻ��A����2��2����B���㣬�ӵ�A�͵�B�ֱ���ƽ����y���ֱ����x��ֱ���C��D���㣬��P��t��0����Ϊ�߶�CD�ϵĶ��㣬����P��ƽ����y���ֱ���������ߺ�ֱ�߷ֱ���R��S��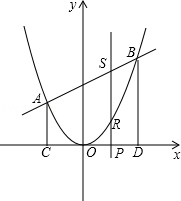
��1����һ�κ����Ͷ��κ����Ľ���ʽ���������B�����ꣻ
��2����SR=2RPʱ�������߶�SR�ij���
��3�����߶�BD����һ����Q����������Ϊt+3�����Ƿ����t��ֵ��ʹS��BRQ=15�������ڣ���t��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4��AD=6��M��N�ֱ���AB��CD�ߵ��е㣬P��AD�ϵĵ㣬����PNB=3��CBN��
��1����֤����PNM=2��CBN��
��2�����߶�AP�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�A����ʱ�뷽����ת���õ�����AEFG��E���������ڱ�CD�ϣ�����BE��BG����BG��AE��P��
��1����֤����CBE=![]() ��BAE��
��BAE��
��2����֤��PG=PB��
��3����AB=![]() ��BC=3�����BG�ij���
��BC=3�����BG�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ջ���д���ɣ�
��1����ͼ�ף��ߡ��� ��=���� ������֪����
��AB��CD���� ����
��2����ͼ�ң���ֱ֪��a��b����3=80�������1����2�Ķ�����
�⣺��a��b������ ����
���1=��4���� ����
�֡ߡ�3=��4���� ����
��3=80������֪��
���1=���� ����������������
�֡ߡ�2+��3=180��
���2=���� ��������ʽ�����ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A�ӵ㣨1��0����������1����λ����/����ٶ���x�����������˶�����O��AΪ����������OABC��ʹ��B��C�ڵ�һ�����ڣ�����AOC=60������P������Ϊ��0��3�������A�˶���t�룬��
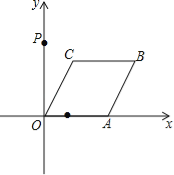
��1����C�����꣨�ú�t�Ĵ���ʽ��ʾ����
��2����A���˶������У���tΪ��ֵʱ��ʹ����OCPΪ���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���д�������� ��
A. ����C=��A�C��B������ABCΪֱ��������
B. ��a��b��c=2��2��2![]() ������ABCΪֱ��������
������ABCΪֱ��������
C. ��a=![]() c��b=
c��b=![]() c������ABCΪֱ��������
c������ABCΪֱ��������
D. ����A�á�B�á�C=3��4��5������ABCΪֱ��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com