
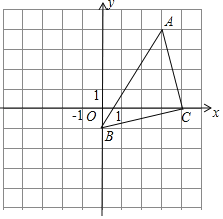
【题目】如图,在平面直角坐标系xOy中,A(3,4),B(0,﹣1),C(4,0).
(1)以点B为中心,把△ABC逆时针旋转90°,画出旋转后的图形![]() ;
;
(2)在(1)中的条件下,
①点C经过的路径弧![]() 的长为 (结果保留π);
的长为 (结果保留π);
②写出点A'的坐标为 .
科目:初中数学 来源: 题型:
【题目】定义:形如y=|G|(G为用自变量表示的代数式)的函数叫做绝对值函数.
例如,函数y=|x﹣1|,y=![]() ,y=|﹣x2+2x+3|都是绝对值函数.
,y=|﹣x2+2x+3|都是绝对值函数.
绝对值函数本质是分段函数,例如,可以将y=|x|写成分段函数的形式:![]() .
.
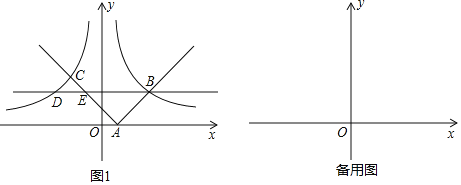
探索并解决下列问题:
(1)将函数y=|x﹣1|写成分段函数的形式;
(2)如图1,函数y=|x﹣1|的图象与x轴交于点A(1,0),与函数y=![]() 的图象交于B,C两点,过点B作x轴的平行线分别交函数y=
的图象交于B,C两点,过点B作x轴的平行线分别交函数y=![]() ,y=|x﹣1|的图象于D,E两点.求证△ABE∽△CDE;
,y=|x﹣1|的图象于D,E两点.求证△ABE∽△CDE;
(3)已知函数y=|﹣x2+2x+3|的图象与y轴交于F点,与x轴交于M,N两点(点M在点N的左边),点P在函数y=|﹣x2+2x+3|的图象上(点P与点F不重合),PH⊥x轴,垂足为H.若△PMH与△MOF相似,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小夏同学从家到学校有![]() ,
,![]() 两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计,早高峰期间,乘坐![]() 线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填
线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填![]() 或
或![]() )线路.
)线路.
查看答案和解析>>
科目:初中数学 来源: 题型:
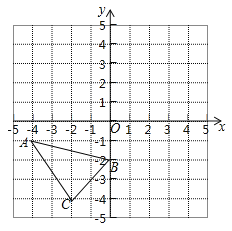
【题目】如图,△ABC的三个顶点都在边长为1的小正方形组成的网格的格点上,以点O为原点建立直角坐标系,回答下列问题:
(1)将△ABC先向上平移5个单位,再向右平移1个单位得到△A1B1C1,画出△A1B1C1,并直接写出A1的坐标 ;
(2)将△A1B1C1绕点(0,﹣1)顺时针旋转90°得到△A2B2C2,画出A2B2C2;
(3)观察图形发现,A2B2C2是由△ABC绕点 顺时针旋转 度得到的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 与y=
与y=![]() 的图象上分别有一点A,B,且AB∥x轴,AD⊥x轴于D,BC⊥x轴于C,若矩形ABCD的面积为8,则b﹣a=( )
的图象上分别有一点A,B,且AB∥x轴,AD⊥x轴于D,BC⊥x轴于C,若矩形ABCD的面积为8,则b﹣a=( )
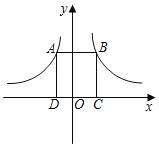
A.8B.﹣8C.4D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有三个小球,上面分别标有数字3、4、5,这些小球除数字不同外其余均相同.
(1)从口袋中随机摸出一个小球,小球上的数字是偶数的概率是______.
(2)从口袋中随机摸出一个小球,记下数字后放回,再随机摸出一个小球,记下数字,请用画树状图(或列表)的方法,求两次摸出的小球上的数字都是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题:
问题:“在平面内,已知分别有2个点,3个点,4个点,5个点,…,![]() 个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
探究:为了解决这个问题,希望小组的同学们,设计了如下表格进行探究:(为了方便研究问题,图中每条线段表示过线段两端点的一条直线)
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有个点时,直线条数为______;
(2)若某同学按照本题中的方法,共画了28条直线,求该平面内有多少个已知点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论正确的是( )
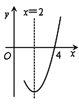
A.当x<2时,y随x增大而增大B.a-b+c<0
C.拋物线过点(-4,0)D.4a+b=0
查看答案和解析>>
科目:初中数学 来源: 题型:
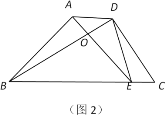
【题目】如图1,在四边形ABCD中,∠BAD=∠BDC=90°,AB=AD,∠DCB=60°,CD=8.
(1)若P是BD上一点,且PA=CD,求∠PAB的度数.
(2)①将图1中的△ABD绕点B顺时针旋转30°,点D落在边BC上的E处,AE交BD于点O,连接DE,如图2,求证:DE2=DODB;
②将图1中△ABD绕点B旋转α得到△A'BD'(A与A',D与D'是对应点),若CD'=CD,则cosα的值为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com