
 轴上一点P(
轴上一点P(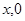 )满足PA+PB最短,则
)满足PA+PB最短,则 .
.科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 垂直的直线l5的函数表达式.
垂直的直线l5的函数表达式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)的图象于点A、B,交x轴于点C.
(x>0)的图象于点A、B,交x轴于点C.
 =
= ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A. | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 中,动点
中,动点 从点
从点 出发,沿
出发,沿 →
→ →
→ →
→ 方向运动至点
方向运动至点 处停止.设点
处停止.设点 运动的路程为
运动的路程为 ,
, 的面积为
的面积为 ,如果
,如果 关于
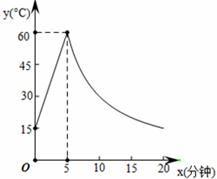
关于 的函数图象如图2所示,则当
的函数图象如图2所示,则当 时,点
时,点 应运动到
应运动到
A. 处 处 | B. 处 处 | C. 处 处 | D. 处 处 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
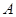 型桌椅售价150元,生产成本100元,运费2元;每套
型桌椅售价150元,生产成本100元,运费2元;每套 型桌椅售价200元,生产成本120元,运费4元,求总利润
型桌椅售价200元,生产成本120元,运费4元,求总利润 (元)与生产
(元)与生产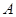 型桌椅
型桌椅 (套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润
(套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润 售价-生产成本-运费)
售价-生产成本-运费)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com