
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.

(1)点![]() 的坐标为___________;
的坐标为___________;
(2)连结![]() ,求
,求![]() 的正切值;
的正切值;
(3)抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() (
(![]() 、
、![]() 不重合),使
不重合),使![]() 与
与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]()
【解析】
(1)根据题意即可求出点C的坐标,然后根据关于y轴对称的两点坐标关系即可求出结论;
(2)过点![]() 作
作![]() 于
于![]() ,先求出OB和CD,再利用勾股定理求出BC和BD,然后根据三角形面积的两种求法即可求出DM,再利用勾股定理求出BM,即可求出结论.
,先求出OB和CD,再利用勾股定理求出BC和BD,然后根据三角形面积的两种求法即可求出DM,再利用勾股定理求出BM,即可求出结论.
(3)根据对称轴公式即可求出二次函数的解析式,然后根据全等三角形的对应情况分类讨论,分别画出对应的图形,然后根据全等三角形的性质、锐角三角函数、平行四边形的判定及性质即可求出结论.
解:(1)∵点![]() ,点
,点![]() 为
为![]() 中点,
中点,
∴点C的坐标为(-1,0)
∵点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
∴点D的坐标为![]() .
.
故答案为:![]() .
.
(2)如图,过点![]() 作
作![]() 于
于![]() ,
,
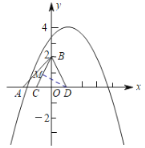
由题易得,![]() ,
,![]() ,
,![]() ,
,
又![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
∴![]() .
.
(3)由题可得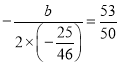 ,
,
解得![]() ,
,
则抛物线所对应的函数解析式为![]() ,
,
①如图,当![]() 时,因为点
时,因为点![]() 不与点
不与点![]() 重合,则点
重合,则点![]() 只能在
只能在![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴于
轴于![]() ,
,
由全等的性质可知,![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
又![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,此时点
,此时点![]() 在抛物线上,且符合题意;
在抛物线上,且符合题意;
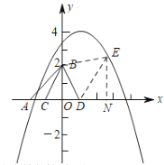
②如图,当![]() ,且点
,且点![]() 在
在![]() 的右侧时,
的右侧时,
易得四边形![]() 是平行四边形,则
是平行四边形,则![]() ,
,
此时点![]() 在抛物线上,且符合题意;
在抛物线上,且符合题意;
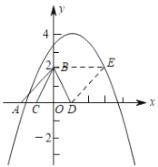
③如图,当![]() ,且点
,且点![]() 在
在![]() 的左侧时,记此时的点
的左侧时,记此时的点![]() 为
为![]() ,
,
则![]() 与①中的
与①中的![]() 组成平行四边形
组成平行四边形![]() ,
,
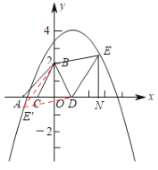
易得![]() ,此时点
,此时点![]() 在抛物线上,且符合题意;
在抛物线上,且符合题意;
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
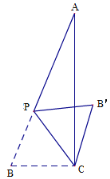
【题目】如图,在△ABC 中,∠ACB=90°,AC=12,BC=5,P 是边 AB 上的动点(不与点 B 重合),将△BCP 沿 CP 所在的直线翻折,得到△B'CP,连接 B'A,B'A 长度的最小值是 m,B'A 长度的最大值是 n,则 m+n 的值等于 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】装商店销售![]() 台
台![]() 型和
型和![]() 台
台![]() 型电脑的利润为
型电脑的利润为![]() 元,销售
元,销售![]() 台
台![]() 型和
型和![]() 台,
台, ![]() 型电脑的利润为
型电脑的利润为![]() 元.
元.
(1)求每台![]() 型电脑和
型电脑和![]() 型电脑的销售利润;
型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共 ![]() 台,其中
台,其中![]() 型电脑的进货量不超过
型电脑的进货量不超过![]() 型电脑的
型电脑的![]() 倍,购进
倍,购进![]() 型电脑
型电脑![]() 台,这
台,这![]() 台电脑的销售总利润为
台电脑的销售总利润为![]() 元.间该商店购进
元.间该商店购进![]() 型
型![]() 服各多少台.才能使销售利润
服各多少台.才能使销售利润![]() 最大?
最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
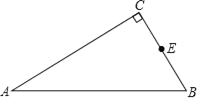
【题目】已知,如图,△ABC中,∠C=90°,E为BC边中点.
(1)尺规作图:以AC为直径,作⊙O,交AB于点D(保留作图痕迹,不需写作法).
(2)连结DE,求证:DE为⊙O的切线;
(3)若AC=5,DE=![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() 是
是![]() 上一点,点
上一点,点![]() 从点
从点![]() 沿折线
沿折线![]() 运动到点
运动到点![]() 时停止;点
时停止;点![]() 从点
从点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,速度均为每秒1个单位长度.如果点
时停止,速度均为每秒1个单位长度.如果点![]() ,
,![]() 同时开始运动,设运动时间为
同时开始运动,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,已知
,已知![]() 与
与![]() 的函数图象如图2所示,有以下结论:
的函数图象如图2所示,有以下结论:
①![]() ;
;
②![]() ;
;
③当![]() 时,
时,![]() ;
;
④当![]() 时,
时,![]() 是等腰三角形;
是等腰三角形;
⑤当![]() 时,
时,![]() .
.
其中正确的有( ).

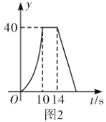
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提升干线公路美化度,相关部门拟定派一个工程队对39000米的公路进行路面“白改黑”工程.该工程队计划使用一大一小两种型号设备交替的方式施工,原计划小型设备每小时铺设路面30米,大型设备每小时铺设路面60米
(1)由于小型设备工作效率较低,该工程队计划使用大型设备的时间比使用小型设备的时间多![]() ,当这个工程完工时,小型设备的使用时间至少为多少小时?
,当这个工程完工时,小型设备的使用时间至少为多少小时?
(2)通过勘察、又新增了部分支线公路美化,结果此工程的实际施工里程比最初拟定的最少里程39000米多了9000米,于是在实际施工中,小型设备在铺设公路效率不变的情况下,使用时间比(1)中的最小值多![]() ,同时,因为工人操作大型设备不够熟练,使得大型设备铺设公路的效率比原计划下降了
,同时,因为工人操作大型设备不够熟练,使得大型设备铺设公路的效率比原计划下降了![]() ,使用时间比(1)中大型设备使用的最短时间多
,使用时间比(1)中大型设备使用的最短时间多![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com