
 在△ABC中,∠ABC=90°,D为AC中点,将线段DC绕点D旋转,得到线段DE,连接AE,CE;
在△ABC中,∠ABC=90°,D为AC中点,将线段DC绕点D旋转,得到线段DE,连接AE,CE;分析 (1)有旋转得出DC=DE,又由中点得出DA=DC,从而得出DE=$\frac{1}{2}$AC,即可;
(2)先判断出点A,B,C,E四点共圆,用同弧所对的圆周角和圆心角的关系即可得出∠ADE=∠CDE=90°,
(3)先判断出∠CAN=∠ECM,从而得出△ACN∽△CEM,求出CN,再用等腰直角三角形的性质得出CH.
解答 解:(1)∵将线段DC绕点D旋转,得到线段DE,
∴DC=DE,
∵D为AC中点,
∴DA=DC,
∴DE=$\frac{1}{2}$AC,
∴△ACE是直角三角形,
(2)如图1,以AC为直径作圆,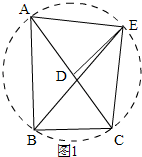
由(1)有,△ACE是直角三角形,
∴∠AEC=90°,
∵∠ABC=90°,
∴∠ABC+∠AEC=180°,
∴点A,B,C,E四点共圆,
∵点D是AC中点,
∴点D是圆心,
∵BE平分∠ABC,
∴∠ABE=∠CBE=45°,
∴$\widehat{AE}=\widehat{CE}$,
∴∠ADE=∠CDE=90°,
∴ED⊥AC,
(3)如图2,延长AH交圆与N,连接CN,
由(2)∠ADE=90°,
∴∠CAE=45°,
∴∠CAN+∠EAN=45°,
∵∠AHC=135°,
∴∠CHN=45°,
∵AC为⊙D的直径,
∴∠ANC=90°,
∴∠NCM=45°,
∴∠MCE+∠NCE=45°,
∵∠EAN=∠ECN,
∴∠CAN=∠ECM,
∵∠ANC=∠CME,
∴△ACN∽△CEM,
∴$\frac{AC}{CE}=\frac{CN}{EM}$,
∵△CDE是等腰直角三角形,
∴CE=$\sqrt{2}$CD,
∵AC=2CD,EM=3,
∴$\frac{2CD}{\sqrt{2}CD}=\frac{CN}{3}$,
∴CN=3$\sqrt{2}$,
∵△CNH为等腰直角三角形,
∴CH=$\sqrt{2}$CN=6.
点评 此题是几何变换综合题,主要考查了直角三角形的判定和性质,等腰直角三角形的判定和性质,相似三角形的性质和判定,四点共圆的判定,解本题的关键是判断出点A,B,C,E四点共圆,判断△ACN∽△CEM是解本题的难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 90 | 90 |
| 面试 | 100 | 70 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李东东在一次钓鱼比赛中,荣获冠军,如图是他根据钓获的鱼的情况绘制的频数分布直方图,根据图示回答下列问题:
李东东在一次钓鱼比赛中,荣获冠军,如图是他根据钓获的鱼的情况绘制的频数分布直方图,根据图示回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
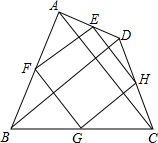 四边形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点
四边形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com