
【题目】已知抛物线![]() .
.
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求其解析式;
(3)设点![]() ,
,![]() 在抛物线上,若
在抛物线上,若![]() ,求m的取值范围.
,求m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)当a>0时,
;(3)当a>0时,![]() ;当a<0时,
;当a<0时,![]() 或
或![]() .
.
【解析】
(1)将二次函数化为顶点式,即可得到对称轴;
(2)根据(1)中的顶点式,得到顶点坐标,令顶点纵坐标等于0,解一元二次方程,即可得到![]() 的值,进而得到其解析式;
的值,进而得到其解析式;
(3)根据抛物线的对称性求得点Q关于对称轴的对称点,再结合二次函数的图象与性质,即可得到![]() 的取值范围.
的取值范围.
(1)∵![]() ,
,
∴![]() ,
,
∴其对称轴为:![]() .
.
(2)由(1)知抛物线的顶点坐标为:![]() ,
,
∵抛物线顶点在![]() 轴上,
轴上,
∴![]() ,
,
解得:![]() 或
或![]() ,
,
当![]() 时,其解析式为:
时,其解析式为:![]() ,
,
当![]() 时,其解析式为:
时,其解析式为:![]() ,
,
综上,二次函数解析式为:![]() 或
或![]() .
.
(3)由(1)知,抛物线的对称轴为![]() ,
,
∴![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
当a>0时,若![]() ,
,
则-1<m<3;
当a<0时,若![]() ,
,
则m<-1或m>3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
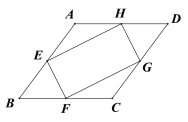
A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.
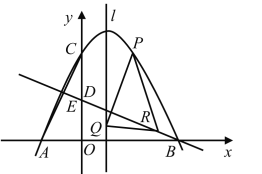
(1)求该抛物线的解析式;
(2)经过点B的直线交y轴于点D,交线段![]() 于点E,若
于点E,若![]() .
.
①求直线![]() 的解析式;
的解析式;
②已知点Q在该抛物线的对称轴l上,且纵坐标为1,点P是该抛物线上位于第一象限的动点,且在l右侧.点R是直线![]() 上的动点,若
上的动点,若![]() 是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽为更好的掌握一元二次方程根的判断情况,两人玩一个游戏:
在一个不透明口袋中装有分别标有 -1,0,1,2的四个小球,除了数字不同之外,这些小球完全一样.
(1)从中任取1球,此小球是非负数的概率是__________.
(2)小明从四球中任取两球,数字和记为m,若一元二次方程![]() 有实根,小明赢,无实根小丽赢.这个游戏公平吗?请你用树状图或列举法分别求出小明、小丽赢的概率,并说明理由.
有实根,小明赢,无实根小丽赢.这个游戏公平吗?请你用树状图或列举法分别求出小明、小丽赢的概率,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点![]() 到以原点为圆心,以1为半径的圆的距离为_____.
到以原点为圆心,以1为半径的圆的距离为_____.
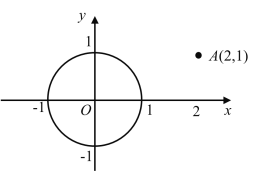
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
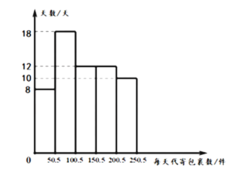
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
(1)如图1,连接CD,求线段CD的长;
(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+![]() EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C绕点B2旋转一周在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com