
 (1)计算:(-3)0-$\sqrt{27}$+|1-$\sqrt{2}$|+$\frac{1}{\sqrt{3}+\sqrt{2}}$
(1)计算:(-3)0-$\sqrt{27}$+|1-$\sqrt{2}$|+$\frac{1}{\sqrt{3}+\sqrt{2}}$分析 (1)先计算零指数幂、化简二次根式、取绝对值、分母有理化,然后根据二次根式的混合运算法则进行解答;
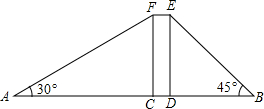
(2)设楼高为x,则CF=DE=x,在Rt△ACF和Rt△DEB中分别用x表示AC、BD的值,然后根据AC+CD+BD=130米,求出x的值即可.
解答 解:(1)原式=1-3$\sqrt{3}$+$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$,
=2$\sqrt{3}$;
(2)设楼高为x米,∵∠B=45°,
∴DB=DE=x.
∵四边形FCDE是矩形,
∴FC=DE=x,
在Rt△AFC中,∵∠A=30°,∴AF=2FC=2x.
由勾股定理得,AC=$\sqrt{3}$x米,
又∵AC+CD+DB=130米,即$\sqrt{3}$x+x=130-10
解得x=$\frac{120}{\sqrt{3}+1}$=60$\sqrt{3}$-60(米),
∴楼高(60$\sqrt{3}$-60)米.
点评 本题考查了二次根式的混合运算,零指数幂以及勾股定理的应用,解答(2)题的关键是构造直角三角形,利用方程思想求解,难度一般.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
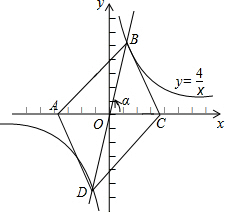 如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕原点O逆时针旋转α度(0<α<90)后的图形,若它与反比例函数y=$\frac{4}{x}$的图象分别交一、三象限的点B、D,已知点A(-m,0)、C(m,0)(m>0)
如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕原点O逆时针旋转α度(0<α<90)后的图形,若它与反比例函数y=$\frac{4}{x}$的图象分别交一、三象限的点B、D,已知点A(-m,0)、C(m,0)(m>0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种货车 | 乙种货车 | |
| 载货量(吨/辆) | 45 | 30 |
| 租金(元/辆) | 400 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
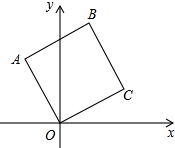 如图,在平面直角坐标系中,四边形ABCO是正方形,已知点C的坐标为($\sqrt{3}$,1),则点B的坐标为( )
如图,在平面直角坐标系中,四边形ABCO是正方形,已知点C的坐标为($\sqrt{3}$,1),则点B的坐标为( )| A. | ($\sqrt{3}$-1,$\sqrt{3}$+1) | B. | ($\sqrt{3}$-1,1) | C. | (1,$\sqrt{3}$+1) | D. | ($\sqrt{3}$-1,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5×10-6 | B. | 25×10-5 | C. | 2.5×10-4 | D. | 2.5×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
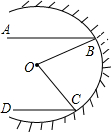 如图是汽车灯的剖面图,从O点发出的光纤照射到凹面镜上,反射出的光线BA、CD是互相平行的水平线,若∠DCO=50°,∠ABD=α,则∠BOC的度数为50°+α(用含α的式子表示).
如图是汽车灯的剖面图,从O点发出的光纤照射到凹面镜上,反射出的光线BA、CD是互相平行的水平线,若∠DCO=50°,∠ABD=α,则∠BOC的度数为50°+α(用含α的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com