练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

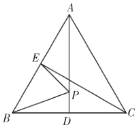
    【题目】如图，在中，，、是的两条中线，是上一个动点，当点运动到某一位置时，可使△PBE的周长最小，则这个最小值为_____．

    【答案】

    【解析】

    △PBE的周长=BE+PB+PE，BE为定值，要使周长最小，则PB+PE最小，转化为“将军饮马”问题，当C，P，E三点共线时，PB+PE=CE最小，求出CE即可．

    如图设CE与AD交于点P'，连接BP'

    ∵△PBE的周长=BE+PB+PE，BE为定值，

    ∴要使周长最小，则PB+PE最小，

    ∵在中，

    ∴△ABC为等边三角形，

    又∵AD、CE为中线

    ∴AD⊥BC，CE⊥AB，

    即AD垂直平分BC，

    当P点运动到P'时，P'B+P'E=CE最小

    在Rt△BCE中，BC=6，BE=AB=3cm

    ∴cm

    ∴△PBE的周长的最小值= BE+CE=cm

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】初三（1）班要从2男2女共4名同学中选人做晨会的升旗手．

    （1）若从这4人中随机选1人，则所选的同学性别为男生的概率是　 　．

    （2）若从这4人中随机选2人，求这2名同学性别相同的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

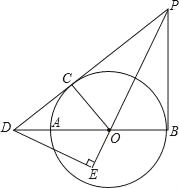
    【题目】如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接PB，∠EDB=∠EPB．

    （1）求证：PB是⊙O的切线．

    （2）若PB=3，DB=4，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

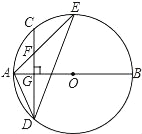
    【题目】如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED； ②FG=2；③tan∠E=； ④S△DEF=4，其中正确的是（　　）

    A. ①②③ B. ①②④ C. ②③④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

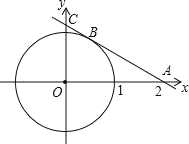
    【题目】如图，圆 O 的半径为 1，过点 A(2，0)的直线与圆 O 相切于点 B，与 y 轴相交于点 C．

    (1)求 AB 的长；

    (2)求直线 AB 的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

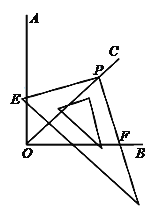
    【题目】如图，∠AOB=90°，将三角尺的直角顶点P落在∠AOB的平分线OC的任意一点上，使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。证明：PE=PF。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．

    （1）试判断直线BC与⊙O的位置关系，并说明理由；

    （2）若BD=2，BF=2，求阴影部分的面积（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，若△ABC内一点P满足∠PAC=∠PCB=∠PBA，则称点P为△ABC的布罗卡尔点，三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现，后来被数学爱好者法国军官布罗卡尔重新发现，并用他的名字命名，布罗卡尔点的再次发现，引发了研究“三角形几何”的热潮．已知△ABC中，CA=CB，∠ACB=120°，P为△ABC的布罗卡尔点，若PA=，则PB+PC=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

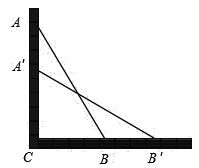
    【题目】如图，一架长2.5m的梯子AB斜靠在墙AC上，∠C=90°，此时，梯子的底端B离墙底C的距离BC为0.7m．

    （1）求此时梯子的顶端A距地面的高度AC；

    （2）如果梯子的顶端A下滑了0.9m，那么梯子的顶端B在水平方向上向右滑动了多远？

    查看答案和解析>>

    同步练习册答案