
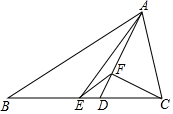
 如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为3.5.
如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,过点C作CF⊥AD于F,连接EF,则线段EF的长为3.5. 分析 首先证明△AGF≌△ACF,则AG=AC=4,GF=CF,证明EF是△BCG的中位线,利用三角形的中位线定理即可求解.
解答  解:延长CF交AB于点G.、
解:延长CF交AB于点G.、
∵AD平分∠BAC,
∴∠GAF=∠CAF,∵CG⊥AD,
∴∠AFG=∠AFC,
在△AGF和△ACF中,$\left\{\begin{array}{l}{∠GAF=∠CAF}\\{AF=AF}\\{∠AFG=∠AFC}\end{array}\right.$,
∴△AGF≌△ACF(ASA),
∴AG=AC=5,GF=CF,
则BG=AB-AG=12-5=7.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=$\frac{1}{2}$BG=3.5.
故答案是:3.5
点评 本题考查了全等三角形的判定以及三角形的中位线定理,证明三角形全等是解决问题的突破口.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
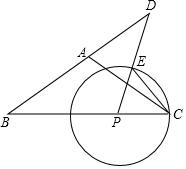 如图,在△ABC中,AB=AC=5,cosB=$\frac{4}{5}$,点P为边BC上一动点,过点P作射线PE交射线BA于点D,∠BPD=∠BAC,以点P为圆心,PC长为半径作⊙P交射线PD于点E,联结CE,设BD=x,CE=y.
如图,在△ABC中,AB=AC=5,cosB=$\frac{4}{5}$,点P为边BC上一动点,过点P作射线PE交射线BA于点D,∠BPD=∠BAC,以点P为圆心,PC长为半径作⊙P交射线PD于点E,联结CE,设BD=x,CE=y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
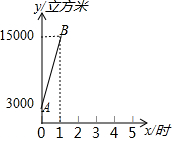 为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00,燃气公司给该市城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气.储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.
为节约能源,某市众多车主响应号召,将燃油汽车改装为天然气汽车.某日上午7:00-8:00,燃气公司给该市城西加气站的储气罐加气,8:00 加气站开始为前来的车辆加气.储气罐内的天然气总量y(立方米)随加气时间x(时)的变化而变化.| 时刻 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 |
| y(立方米) | 15000 | 7500 | 5000 | 3750 | 3000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某学校为了加固一篮球架,在下面焊接了一根钢筋撑杆AC,它与水平的钢板箱体成60°的夹角,且AB=0.5m.原有的上撑杆DE=1.6m,且∠BDE=135°.
如图,某学校为了加固一篮球架,在下面焊接了一根钢筋撑杆AC,它与水平的钢板箱体成60°的夹角,且AB=0.5m.原有的上撑杆DE=1.6m,且∠BDE=135°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com