
先阅读,再解题:
对于一元二次方程 ,
,
通过配方可将方程变形为
∵a¹
0,∴ .
.
完成下列填空:
(1)方程 的根的情况取决于________的值的符号.
的根的情况取决于________的值的符号.
(2)某同学判断关于x的方程 的根的情况如下:
的根的情况如下:
解: ①
①
=-16k ②
∵-16k<0 ③
∴ ④
④
∴原方程无实数根. ⑤
请判断他的解答是否正确,并写出你的判断理由.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:阅读理解
| x |
| x-1 |
| x |
| x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省扬州市邗江区七年级下学期期中考试数学试卷(带解析) 题型:解答题
阅读与理解:
(1)先阅读下面的解题过程:
分解因式: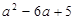
解:方法(1)原式



方法(2)原式



再请你参考上面一种解法,对多项式进 行因式分解;
行因式分解;
(2)阅读下面的解题过程:
已知 :,试求
:,试求 与
与 的值。
的值。
解:由已知得:
因此得到:
所以只有当 并且
并且 上式才能成立。
上式才能成立。
因而得: 并且
并且
请你参考上面的解题方法解答下面的问题:
已知: ,试求
,试求 的值
的值
查看答案和解析>>
科目:初中数学 来源:2015届江苏省扬州市邗江区七年级下学期期中考试数学试卷(解析版) 题型:解答题
阅读与理解:
(1)先阅读下面的解题过程:
分解因式:
解:方法(1)原式



方法(2)原式



再请你参考上面一种解法,对多项式进 行因式分解;
行因式分解;
(2)阅读下面的解题过程:
已知 :,试求
:,试求 与
与 的值。
的值。
解:由已知得:
因此得到:
所以只有当 并且
并且 上式才能成立。
上式才能成立。
因而得: 并且
并且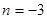
请你参考上面的解题方法解答下面的问题:
已知: ,试求
,试求 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com