
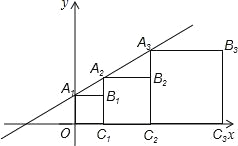
【题目】在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是 ,点Bn的坐标是 .
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
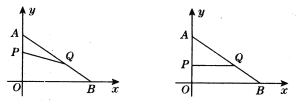
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,关于x的方程:x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() 的解是x1=c,x2=﹣
的解是x1=c,x2=﹣![]() ;x+
;x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解是x1=c,x2=
的解是x1=c,x2=![]() ;……
;……
(1)请观察上述方程与解的特征,比较关于x的方程x+![]() =c+
=c+![]() (a≠0)与它们的关系猜想它的解是什么,并利用“方程的解”的概念进行验证.
(a≠0)与它们的关系猜想它的解是什么,并利用“方程的解”的概念进行验证.
(2)可以直接利用(1)的结论,解关于x的方程:x+![]() =a+
=a+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明经过市场调查,整理出他妈妈商店里一种商品在第![]() 天的销售量的相关信息如下表:
天的销售量的相关信息如下表:
时间第 |
|
|
售价(元/件) |
| 50 |
每天销量(件) |
| |
已知该商品的进价为每件20元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=10,高AD=8,M、N、P分别在边AB、BC、AC上移动,但不与A、B、C重合,连接MN、NP、MP,且MP始终与BC保持平行,AD与MP相交于点E,设MP=x,△MNP的面积用y表示.
(1)求y关于x的函数关系式;
(2)当x取什么值时,y有最大值,并求出的最大值;
(3)当x取什么值时,△MNP是等腰直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车可达1440辆次;若停车费超过5元,则每超过1元,每天来此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费﹣每天的固定支出)
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地盛产樱桃,一年一度的樱桃节期间,很多果园推出了免费品尝和优惠采摘活动,其中甲、乙两家果园的樱桃品质相同,销售价格也相同,但推出了不同的采摘方案:
甲园 | 游客进园需购买 |
乙园 | 游客进园不需购买门票,采摘的樱桃在一定数量以内按原价购买,超过部分打折购买 |
小明和爸爸、妈妈在樱桃节期间也来采摘樱桃,若设他们的樱桃采摘量为![]() (千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为
(千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为![]() (元)在乙采摘园所需总费用为
(元)在乙采摘园所需总费用为![]() (元),图中的折线
(元),图中的折线![]() 表示
表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)①甲、乙两果园的樱桃单价为_____________元![]() 千克;
千克;
②直接写出![]() 的函数表达式:_________________,并在图中补画出
的函数表达式:_________________,并在图中补画出![]() 的函数图象;
的函数图象;
(2)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若小明一家当天所采摘的樱桃不少于![]() 千克,选择哪个采摘园更划算?请说明理由.
千克,选择哪个采摘园更划算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
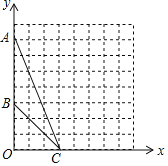
(1)在图中作出△ABC的外接圆⊙P(保留必要的作图痕迹,不写作法)
(2) 若在x轴的正半轴上有一点D(异与C点),且∠ADB=∠ACB,则点D的坐标为 .
(3)若用扇形PAC围成一个圆锥,那么这个圆锥的底面半径为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com