
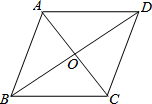
 如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )| A. | 5cm | B. | 10cm | C. | 14cm | D. | 20cm |
分析 根据菱形的对角线互相垂直平分可得AC⊥BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,再利用勾股定理列式求出AB,然后根据菱形的四条边都相等列式计算即可得解.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3cm,
OB=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4cm,
根据勾股定理得,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5cm,
所以,这个菱形的周长=4×5=20cm.
故选D.
点评 本题考查了菱形的性质,勾股定理,主要利用了菱形的对角线互相垂直平分,需熟记.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
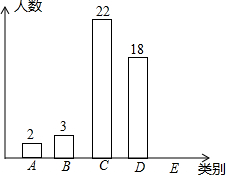 某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).
某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{12}$ | C. | $\sqrt{a^2}$ | D. | $\sqrt{\frac{1}{a}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
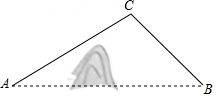 A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
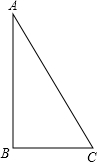 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( )| A. | l1:l2=1:2,S1:S2=1:2 | B. | l1:l2=1:4,S1:S2=1:2 | ||
| C. | l1:l2=1:2,S1:S2=1:4 | D. | l1:l2=1:4,S1:S2=1:4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com