练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图11，试比较图中两个几何图形的异同，请分别写出它们的两个相同点和两个不同点．

    例如：相同点：正方形的对角线相等，正五边形的对角线也相等．

    不同点：正方形有四条边，而正五边形有五条边．

    相同点：（1）____________________；（2）____________________；

    不同点：（1）____________________；（2）____________________．

    答案不惟一．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

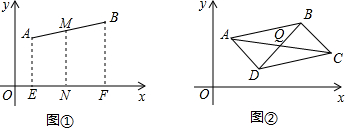    让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系．
    第一步：数轴上两点连线的中点表示的数．自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是
    1
    1
    ． 再试几个，我们发现：数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数．
    第二步；平面直角坐标系中两点连线的中点的坐标（如图①）为便于探索，我们在第一象限内取两点A（x1，y1），B（x2，y2），取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（
    x1+x2
    2
    x1+x2
    2
    ，
    y1+y2
    2
    y1+y2
    2
     ）（用x1，y1，x2，y2表示），AEFB是矩形时也可以．我们的结论是：平面直角坐标系中连接两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数．
    第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）在平面直角坐标系中画一个平行四边形ABCD，设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），则其对角线交点Q的坐标可以表示为Q（
    x1+x3
    2
    x1+x3
    2
    ，
    y1+y3
    2
    y1+y3
    2
    ），也可以表示为Q（
    x2+x4
    2
    x2+x4
    2
    ，
    y2+y4
    2
    y2+y4
    2
     ），经过比较，我们可以分别得出关于x1，x2，x3，x4及，y1，y2，y3，y4的两个等式是
    x1+x3=x2+x4
    x1+x3=x2+x4
    和
    y1+y3=y2+y4
    y1+y3=y2+y4
    ． 我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的
    和相等
    和相等
    ．

    查看答案和解析>>

    科目：初中数学 来源：101网校同步练习　初三数学　华东师大(新课标2001/3年初审) 华东师大版 题型：044

    如图，在空间中，与定点的距离等于定长的点的集合叫做球面．定点叫做球心，定长叫做半径．球面被经过球心的平面截得的圆叫做大圆．

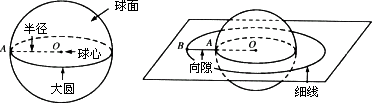
    探究1：当我们把半径为11 cm的足球看成一个球时，假设有一根无弹性的细线恰好能沿足球的大圆紧紧缠绕一周，将细线的长度增加1米后，细线仍以圆形呈现，且圆心为足球的球心．若将细线与足球表面的间隙记为h1(间隙如图所示)，求h1的长；(π取3.14，结果精确到1 cm)

    探究2：将探究1中的足球分别换成乒乓球和地球，其他条件都不改变．设乒乓球的半径为r，细线与乒乓球表面的间隙为h2；地球的半径为R，细线与地球表面的间隙为h3，试比较h2与h3的大小，并说明理由．

    查看答案和解析>>

    同步练习册答案