
����Ŀ�����ž��õĿ��ٷ�չ����������Խ��Խ�ܵ����ǵĹ�ע��ijУѧ����Ϊ���˽���������֪ʶ���ռ��������������˲���ѧ������������Ϊ���dz��˽������˽������˽�����������˽������࣬�������������Ƴ���������ͳ��ͼ��
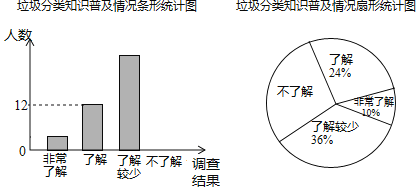
��1�����α������ѧ���ж���������ȫ����ͳ��ͼ��
��2�����Ƹ�У1200��ѧ�������dz��˽��������˽������������Ƕ��٣�
��3������������dz��˽�����ѧ������2������������ΪŮ�������������ȡ2����ȫУ����������֪ʶ�����������û���״ͼ���б��ķ�������ǡ�ó鵽һ��һŮ�ĸ��ʣ�
���𰸡���1�����α������ѧ����50�ˣ���ȫͼ�μ���������2�����Ƹ�У1200��ѧ�������dz��˽��������˽�������������408�ˣ���3��ǡ�ó鵽һ��һŮ�ĸ���Ϊ![]() ��
��
��������
��1�������˽���������������ռ�ٷֱ���������������������Զ�Ӧ�İٷֱȿ�������dz��˽��������˽���������������̶���������˽������������Ӷ���ȫͼ�Σ�
��2������������������˼�����ɵã�
��3������״ͼչʾ����20�ֵȿ��ܵĽ���������ҳ����������Ľ������Ȼ�����ø��ʹ�ʽ��⣮
��1�����α������ѧ������12��24%��50���ˣ���
�����dz��˽���������Ϊ50��10%��5���ˣ���
���˽������������Ϊ50��36%��18���ˣ���
�����˽���������Ϊ50����5+12+18����15���ˣ���
��ȫͼ�����£�

��2�����Ƹ�У1200��ѧ�������dz��˽��������˽�������������1200��![]() ��408���ˣ���
��408���ˣ���
��3������״ͼΪ��
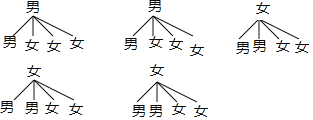
����20�ֵȿ��ܵĽ����������ǡ�ó鵽һ��һŮ����12�ֽ����
����ǡ�ó鵽һ��һŮ�ĸ���Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��1��0����B��0��3��������AOB�Ƶ�O��ʱ����ת90�㣬�õ���COD����EΪAD���е㣮

��1���ж�AB��CD�Ĺ�ϵ��֤����
��2����ֱ��EC�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ���е㣬��
���е㣬��![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() ���ۣ�ʹ�õ�
���ۣ�ʹ�õ�![]() ���ڵ�
���ڵ�![]() ������
������![]() ʱ����ô
ʱ����ô![]() �ij�Ϊ________________��
�ij�Ϊ________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı��ε������Խ����������Ϊ60�������dz��������ı���Ϊ�������ı�������
��1��������ƽ���ı��Ρ����Ρ����Ρ����������У�һ�������������ı����������� ����
��������ABCD���������ı���������AB��4����BC���� ����
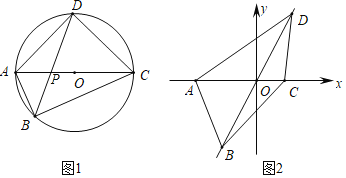
��2����ͼ1���������ı�����ABCD�ڽ��ڡ�O��AC��BD�ཻ�ڵ�P���ҶԽ���ACΪֱ����AP��1��PC��5������һ���Խ���BD�ij���
��3����ͼ2��ƽ��ֱ������ϵ�У���֪�������ı�����ABCD���ĸ�����A����3��0����C ��2��0����B�ڵ������ޣ�D�ڵ�һ���ޣ�AC��BD���ڵ�O��ֱ��BD��б��Ϊ![]() �����ı���ABCD�����Ϊ15
�����ı���ABCD�����Ϊ15![]() �������κ���y��ax2+bx+c��a��b��cΪ��������a��0����ͼ��ͬʱ�������ĸ����㣬��a��ֵ��
�������κ���y��ax2+bx+c��a��b��cΪ��������a��0����ͼ��ͬʱ�������ĸ����㣬��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��3��1����B��1��0����PQ��ֱ��y=x�ϵ�һ�����߶���PQ=![]() ��Q��P���·�������AP+PQ+QBȡ��Сֵʱ����Q����Ϊ______��
��Q��P���·�������AP+PQ+QBȡ��Сֵʱ����Q����Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�⣺(������ͼ�ۼ�����д����)
(1)��֪����ͼ���ı���ABCD���ı���EFGH�����ĶԳƣ��Ի������ǵĶԳ�����O��
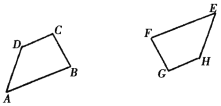
(2)����ѧ���ڿ��Ź����з���һ��Բ�̣�������Ϊ��ʷ�ƾã��Ѿ���һ����ȱʧ����ͼ��ʾ����ϣ����ԭԲ�̣���Ҫ���ҵ�Բ�̵�Բ�ģ����ܼ�����ɺ�����������������ֱ�ߣ��̶ȣ���Բ�棬��ͼ���ҳ�Բ��O.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P(x,y)��������y���������x�IJ�y��x��ΪP��ġ���������ͼ��G�����е�ġ������е����ֵ��Ϊͼ��G�ġ�����ֵ��
(1)�ٵ�A(1,3) �ġ�����Ϊ ��
��������y=��x2+3x+3�ġ�����ֵ��Ϊ ��
(2)ij���κ���y=��x2+bx+c(c��0) �ġ�����ֵ��Ϊ1����B(m,0)���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�ġ�������ȡ�
��ֱ��д��m= (�ú�c��ʽ�ӱ�ʾ)
����˶��κ����ı���ʽ��
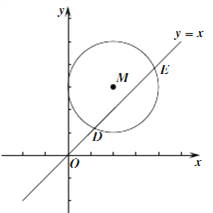
(3)��ͼ����ƽ��ֱ������ϵxOy�У���M(2,3)ΪԲ�ģ�2Ϊ�뾶��Բ��ֱ��y=x�ཻ�ڵ�D��E��ֱ��д����M�ġ�����ֵ��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�̽�������������һ������A���Ƿ������һ������B�������ܳ�������ֱ�����֪�����ܳ��������һ�룿����������пո�
��1������֪����A�ı߳��ֱ�Ϊ6��1ʱ��С��ͬѧ�������о��ģ�
��������ε����߷ֱ���x��y��������÷����飺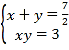 ����ȥy����ã�2x2��7x+6=0��
����ȥy����ã�2x2��7x+6=0��
�ߡ�=49��48��0��
��x1=_____��x2=_______��
������Ҫ��ľ���B���ڣ�
��2�������֪����A�ı߳��ֱ�Ϊ2��1���������С���ķ����о��Ƿ��������Ҫ��ľ���B��
��3���������A�ı߳�Ϊm��n�������о�����ʲô����ʱ������B���ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
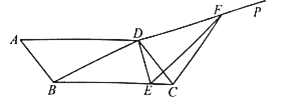
����Ŀ����ͼ����![]() �У�
�У�![]() ���Խ���
���Խ���![]() ����E���߶�BC�ϵĶ��㣬����DE������D��DP��DE��������DP��ȡ��F��ʹ��
����E���߶�BC�ϵĶ��㣬����DE������D��DP��DE��������DP��ȡ��F��ʹ��![]() ������CF,��
������CF,��![]() �ܳ�����СֵΪ___________.
�ܳ�����СֵΪ___________.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com