
如下图,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
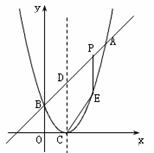
解:(1) ∵ 点A(3,4)在直线y=x+m上,
∴ 4=3+m.
∴ m=1.
设所求二次函数的关系式为y=a(x-1)2.
∵ 点A(3,4)在二次函数y=a(x-1)2的图象上,
∴ 4=a(3-1)2,
∴ a=1.
∴ 所求二次函数的关系式为y=(x-1)2.
即y=x2-2x+1.
(2) 设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP-yE
=(x+1)-(x2-2x+1)
=-x2+3x.
即h=-x2+3x (0<x<3).
(3) 存在.
解法1:要使四边形DCEP是平行四边形,必需有PE=DC.
∵ 点D在直线y=x+1上,
∴ 点D的坐标为(1,2),
∴ -x2+3x=2 .
即x2-3x+2=0 .
解之,得 x1=2,x2=1 (不合题意,舍去)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形.
解法2:要使四边形DCEP是平行四边形,必需有BP∥CE.
设直线CE的函数关系式为y=x+b.
∵ 直线CE 经过点C(1,0),
∴ 0=1+b,
∴ b=-1 .
∴ 直线CE的函数关系式为y=x-1 .
∴ ![]() 得x2-3x+2=0.
得x2-3x+2=0.
解之,得 x1=2,x2=1 (不合题意,舍去)
∴ 当P点的坐标为(2,3)时,四边形DCEP是平行四边形.


科目:初中数学 来源: 题型:
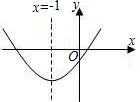 已知二次函数的图象如下图所示,则下列结论:①a+b+c>0;②a-b+c<0;③b=2a;④b2-4ac>0;⑤abc>0,其中正确的个数是( )
已知二次函数的图象如下图所示,则下列结论:①a+b+c>0;②a-b+c<0;③b=2a;④b2-4ac>0;⑤abc>0,其中正确的个数是( )| A、4 | B、3 | C、2 | D、1 |
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第1期 总第157期 沪科版 题型:044
如下图,已知二次函数
y=ax2-4x+c的图象经过点A和点B.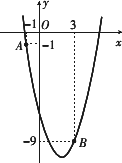
(1)求该二次函数的函数关系式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com