
如图,已知,等腰Rt△OAB中,∠AOB=90o,等腰Rt△EOF中,∠EOF=90o,连结AE、BF.
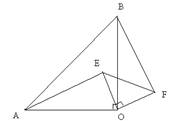
求证:(1)AE=BF;(2)AE⊥BF.
见解析
解析:解:(1)证明:在△AEO与△BFO中,
∵Rt△OAB与Rt△EOF等腰直角三角形,
∴AO=OB,OE=OF,∠AOE=90o-∠BOE=∠BOF,
∴△AEO≌△BFO,
∴AE=BF;
( 2)延长AE交BF于D,交OB于C,则∠BCD=∠ACO, 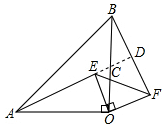
由(1)知:∠OAC=∠OBF,
∴∠BDA=∠AOB=90o,
∴AE⊥BF.
(1)可以把要证明相等的线段AE,CF放到△AEO,△BFO中考虑全等的条件,由两个等腰直角三角形得AO=BO,OE=OF,再找夹角相等,这两个夹角都是直角减去∠BOE的结果,所以相等,由此可以证明△AEO≌△BFO;
(2)由(1)知:∠OAC=∠OBF,∴∠BDA=∠AOB=90°,由此可以证明AE⊥BF


科目:初中数学 来源: 题型:
 22、如图,已知,等腰Rt△OAB中,∠AOB=90°,等腰Rt△EOF中,∠EOF=90°,连接AE、BF.
22、如图,已知,等腰Rt△OAB中,∠AOB=90°,等腰Rt△EOF中,∠EOF=90°,连接AE、BF.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知在等腰Rt△BCD中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E,H是BC边的中点,连接DH与BE相交于点G
如图,已知在等腰Rt△BCD中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E,H是BC边的中点,连接DH与BE相交于点G| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2012届广东省汕头市潮南区中考模拟考试数学卷(带解析) 题型:解答题
如图,已知,等腰Rt△OAB中,∠AOB=90o,等腰Rt△EOF中,∠EOF=90o,连结AE、BF.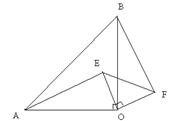
求证:(1)AE=BF;(2)AE⊥BF.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省汕头市潮南区中考模拟考试数学卷(解析版) 题型:解答题
如图,已知,等腰Rt△OAB中,∠AOB=90o,等腰Rt△EOF中,∠EOF=90o,连结AE、BF.
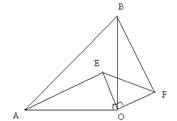
求证:(1)AE=BF;(2)AE⊥BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com