
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第5次操作后得到的折痕D4E4,到BC的距离记为h5;若h1=1,则h5的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第5次操作后得到的折痕D4E4,到BC的距离记为h5;若h1=1,则h5的值为( )| A. | $2-\frac{1}{2^4}$ | B. | $\frac{1}{2^4}$ | C. | $1-\frac{1}{2^5}$ | D. | $\frac{1}{2^5}$ |
分析 根据中点的性质及折叠的性质可得DA=DA'=DB,从而可得∠ADA'=2∠B,结合折叠的性质,∠ADA'=2∠ADE,可得∠ADE=∠B,继而判断DE∥BC,得出DE是△ABC的中位线,证得AA1⊥BC,得到AA1=2,求出h1=2-1=1,同理h2=2-$\frac{1}{2}$,h3=2-$\frac{1}{2}$×$\frac{1}{2}$=2-$\frac{1}{{2}^{2}}$,于是经过第5次操作后得到的折痕D4E4到BC的距离h5=2-$\frac{1}{{2}^{4}}$.
解答 解:连接AA1,
由折叠的性质可得:AA1⊥DE,DA=DA1,
又∵D是AB中点,
∴DA=DB,
∴DB=DA1,
∴∠BA1D=∠B,
∴∠ADA1=2∠B,
又∵∠ADA1=2∠ADE,
∴∠ADE=∠B,
∴DE∥BC,
∴AA1⊥BC,
∴AA1=2,
∴h1=2-1=1,
同理,h2=2-$\frac{1}{2}$,h3=2-$\frac{1}{2}$×$\frac{1}{2}$=2-$\frac{1}{{2}^{2}}$,于是经过第5次操作后得到的折痕D4E4到BC的距离h5=2-$\frac{1}{{2}^{4}}$,
故选A.
点评 本题考查了相似三角形的判定和性质,三角形中位线的性质,平行线等分线段定理,找出规律是解题的关键.


科目:初中数学 来源: 题型:选择题
 在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )
在四边形ABCD中,AB∥CD,∠A=90°,AB=1,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△EDF的面积为( )| A. | 3$\sqrt{2}$-4 | B. | 3$\sqrt{2}$-3 | C. | 3$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | SSS | B. | ASA | C. | SAS | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
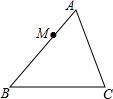 如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=4或6.
如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=4或6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com