
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点(-1,0),对称轴为:直线x=1,则下列结论中正确的是:( )
A.a>0
B.当x>1时,y随x的增大而增大
C.![]() <0
<0
D.x=3是一元二次方程ax2+bx+c=0(a≠0)的一个根
【答案】D
【解析】抛物线 ![]() 的开口向下,则
的开口向下,则 ![]() ,故A不正确;
,故A不正确;
对称轴为 ![]() ,当
,当 ![]() 时,
时, ![]() 随
随 ![]() 的增大而减小,故B不正确;
的增大而减小,故B不正确;
抛物线与 ![]() 轴的交点在
轴的交点在 ![]() 轴的正半轴,则
轴的正半轴,则 ![]() ,故C不正确;
,故C不正确;
抛物线经过点(-1,0),关于对称轴 ![]() 的对称点为(3,0),则
的对称点为(3,0),则 ![]() 是一元二次方程
是一元二次方程 ![]() 的一个根.
的一个根.
所以答案是:D.
【考点精析】通过灵活运用二次函数的性质和抛物线与坐标轴的交点,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点D,E分别在线段AB, AC上,CD与BE相交于O点,已知AD=AE,现添加以下哪个条件仍不能判定△ABE≌△ACD( )

A. BD= CEB. ∠B=∠CC. BE=CDD. AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,直线![]() ,另一直线交
,另一直线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,且
,且![]() ,点
,点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为直线
为直线![]() 上一动点,且
上一动点,且![]() .
.
(![]() )如图
)如图![]() ,当点
,当点![]() 在点
在点![]() 右边且点
右边且点![]() 在点
在点![]() 左边时,
左边时,![]() 的平分线交
的平分线交![]() 的平分线于点
的平分线于点![]() ,求
,求![]() 的度数;
的度数;
(![]() )如图
)如图![]() ,当点
,当点![]() 在点
在点![]() 右边且点
右边且点![]() 在点
在点![]() 右边时,
右边时,![]() 的平分线交
的平分线交![]() 的平分线于点
的平分线于点![]() ,求
,求![]() 的度数;
的度数;
(![]() )当点
)当点![]() 在点
在点![]() 左边且点
左边且点![]() 在点
在点![]() 左边时,
左边时,![]() 的平分线交
的平分线交![]() 的平分线所在直线交于点
的平分线所在直线交于点![]() ,请直接写出
,请直接写出![]() 的度数,不说明理由.
的度数,不说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
①当a=5时,方程组的解是![]() ;
;
②当x,y的值互为相反数时,a=20;
③不存在一个实数a使得x=y;
④若![]() ,则a=2.
,则a=2.
A. ①②③④ B. ②③ C. ②③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A (3,2)、B(1,3)。△AOB绕点O 逆时针旋转90°后得到△A1OB1.
(1)画出旋转后的图形;
(2)求线段OB在旋转过程中所扫过的图形面积(写过程)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 E,F 是ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
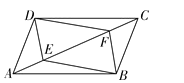
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com