
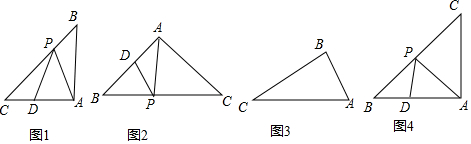
分析 (1)只要证明∠A=∠PAB即可解决问题.
(2)如图3中,作∠BAC的平分线AP交BC于P,作PD∥AB交AC于D,只要证明DP=DA,即可解决问题.
(3)分三种情形讨论①如图3′中,当DA=DP时.②如图4中,当PA=PD时.③如图5中,当AP=AD时.分别求解即可解决问题.
解答 解:(1)如图2中,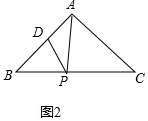
∵AB=AC,DA=DP,
∴∠B=∠C,∠DAP=∠DPA,
∵∠PAC=∠BPD,
∴∠APC=∠BDP=∠DAP+∠DPA,
∵∠APC=∠B+∠BAP,
∴∠B=∠PAB=50°,
∵∠BAC=180°-50°-50°=80°,
∴∠PAC=30°
故答案为30°.
(2)如图3中,作∠BAC的平分线AP交BC于P,作PD∥AB交AC于D,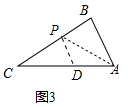
∴∠BAP=∠PAD=∠DPA,∠CPD=∠B,
∵∠CAB=2∠C,
∴∠PAD=∠C,
∴DP=DA,
∴△APD是等腰三角形且与△APB与△CDP相似.
(3)如图3′中,当DA=DP时,设∠APD=∠DAP=x,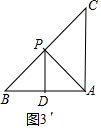
①若∠BPD=∠CAP=90°-x,∠BDP=∠CPA=2x,
∴90°-x+2x+x=180°,
∴x=45°,
∴三角形都是等腰直角三角形,易知AD=1,
②若∠PDB=∠CAP时,设∠APD=∠DAP=x,得到∠PDB=∠CAP=2x,易知x=30°,设AD=a,则AP=$\sqrt{3}$a,
∵△BPD∽△CPA,
∴$\frac{BD}{AC}$=$\frac{PD}{PA}$,即$\frac{2-a}{2}$=$\frac{a}{\sqrt{3}}$a,解得a=$\frac{6-2\sqrt{3}}{3}$,
如图4中,当PA=PD时,易知∠PDB是钝角,∠CAP是锐角,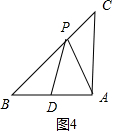
∴∠PDB=∠CPA,则△BPD≌△CPA,设AD=a,则BD=2-a,BP=2$\sqrt{2}$-(2-a),AC=2,
2$\sqrt{2}$-(2-a)=2,
解得a=4-2$\sqrt{2}$,
如图5中,当AP=AD时,设∠APD=∠ADP=x,则∠DAP=180°-2x,易知∠PDB为钝角,∠CAP为锐角,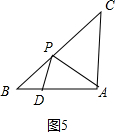
∴∠PDB=∠CAP=180°-x,∠CAP=90°-∠DAP=90°-(180°-2x)=2x-90°,
在△APC中,2x-90°+180°-x+45°=180°,解得x=45°,不可能成立.
综上所述.AD的长为1或$\frac{6-2\sqrt{3}}{3}$或4-2$\sqrt{2}$.
点评 本题考查相似三角形综合题、等腰直角三角形的性质、角平分线的定义、相似三角形的判定和性质等知识,解题的关键是理解题意,学会用构建方程的思想思考问题,属于中考压轴题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠CAB=70°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 35° | B. | 40° | C. | 50° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-3x-9 | B. | y=-3x-2 | C. | y=-3x+2 | D. | y=-3x+9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com