
”¾ĢāÄæ”æ¹ÅŌĖŗÓŹĒŃļÖŻµÄÄøĒ×ŗÓ![]() ĪŖ“ņŌģ¹ÅŌĖŗÓ·ē¹ā“ų£¬ĻÖÓŠŅ»¶Ī³¤ĪŖ180Ć×µÄŗÓµĄÕūÖĪČĪĪńÓÉA”¢BĮ½¹¤³Ģ¶ÓĻČŗó½ÓĮ¦Ķź³É
ĪŖ“ņŌģ¹ÅŌĖŗÓ·ē¹ā“ų£¬ĻÖÓŠŅ»¶Ī³¤ĪŖ180Ć×µÄŗÓµĄÕūÖĪČĪĪńÓÉA”¢BĮ½¹¤³Ģ¶ÓĻČŗó½ÓĮ¦Ķź³É![]() ¹¤³Ģ¶ÓĆæĢģÕūÖĪ12Ć×£¬B¹¤³Ģ¶ÓĆæĢģÕūÖĪ8Ć×£¬¹²ÓĆŹ±20Ģģ£®
¹¤³Ģ¶ÓĆæĢģÕūÖĪ12Ć×£¬B¹¤³Ģ¶ÓĆæĢģÕūÖĪ8Ć×£¬¹²ÓĆŹ±20Ģģ£®
![]() øł¾ŻĢāŅā£¬¼×”¢ŅŅĮ½ĆūĶ¬Ń§·Ö±šĮŠ³öÉŠ²»ĶźÕūµÄ·½³Ģ×éČēĻĀ£ŗ
øł¾ŻĢāŅā£¬¼×”¢ŅŅĮ½ĆūĶ¬Ń§·Ö±šĮŠ³öÉŠ²»ĶźÕūµÄ·½³Ģ×éČēĻĀ£ŗ
¼×£ŗ![]() £»ŅŅ£ŗ
£»ŅŅ£ŗ
øł¾Ż¼×”¢ŅŅĮ½ĆūĪŹŃ§ĖłĮŠµÄ·½³Ģ×飬ĒėÄć·Ö±šÖø³öĪ“ÖŖŹżx”¢y±ķŹ¾µÄŅāŅå£¬Č»ŗóŌŚ·½æņÖŠ²¹Č«¼×”¢ŅŅĮ½ĆūĶ¬Ń§ĖłĮŠµÄ·½³Ģ×é£ŗ
¼×£ŗx±ķŹ¾______£¬y±ķŹ¾______£»
ŅŅ£ŗx±ķŹ¾______£¬y±ķŹ¾______£®
![]() ĒóA”¢BĮ½¹¤³Ģ¶Ó·Ö±šÕūÖĪŗÓµĄ¶ąÉŁĆ×
ĒóA”¢BĮ½¹¤³Ģ¶Ó·Ö±šÕūÖĪŗÓµĄ¶ąÉŁĆ×![]() Š“³öĶźÕūµÄ½ā“š¹ż³Ģ
Š“³öĶźÕūµÄ½ā“š¹ż³Ģ![]()
”¾“š°ø”æ£Ø1£©20£»180£»180£»20£»A¹¤³Ģ¶ÓÓƵď±¼ä£»B¹¤³Ģ¶ÓÓƵď±¼ä£»A¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏ż£»B¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏ż.£Ø2£©60Ć×£»120Ć×.
”¾½āĪö”æ
£Ø1£©“ĖĢāŌĢŗ¬Į½øö»ł±¾ŹżĮæ¹ŲĻµ£ŗA¹¤³Ģ¶ÓÓƵď±¼ä+B¹¤³Ģ¶ÓÓƵď±¼ä=20Ģģ£¬A¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏ż+B¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏ż=180Ć×£¬ÓÉ“Ė½ųŠŠ½ā“š¼“æÉ£»
£Ø2£©Ń”ŌńĘäÖŠŅ»øö·½³Ģ×é½ā“šĪŹĢā.
£Ø1£©¼×Ķ¬Ń§£ŗÉčA¹¤³Ģ¶ÓÓƵď±¼äĪŖ![]() Ģģ£¬B¹¤³Ģ¶ÓÓƵď±¼äĪŖ
Ģģ£¬B¹¤³Ģ¶ÓÓƵď±¼äĪŖ![]() Ģģ£¬ÓÉ“ĖĮŠ³öµÄ·½³Ģ×éĪŖ
Ģģ£¬ÓÉ“ĖĮŠ³öµÄ·½³Ģ×éĪŖ![]() £»
£»
ŅŅĶ¬Ń§£ŗA¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏żĪŖ![]() £¬B¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏żĪŖ
£¬B¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏żĪŖ![]() £¬ÓÉ“ĖĮŠ³öµÄ·½³Ģ×éĪŖ
£¬ÓÉ“ĖĮŠ³öµÄ·½³Ģ×éĪŖ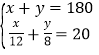 £»
£»
¹Ź“š°øŅĄ“ĪĪŖ£ŗ![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() £¬A¹¤³Ģ¶ÓÓƵď±¼ä£¬B¹¤³Ģ¶ÓÓƵď±¼ä£¬A¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏ż£¬B¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏ż.
£¬A¹¤³Ģ¶ÓÓƵď±¼ä£¬B¹¤³Ģ¶ÓÓƵď±¼ä£¬A¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏ż£¬B¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏ż.
£Ø2£©Ń”¼×Ķ¬Ń§ĖłĮŠ·½³Ģ×é½ā“šČēĻĀ£ŗ
![]() £¬
£¬
![]() µĆ
µĆ![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
°Ń![]() “śČė
“śČė![]() µĆ£ŗ
µĆ£ŗ![]() £¬
£¬
ĖłŅŌ·½³Ģ×éµÄ½āĪŖ![]() £¬
£¬
A¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏żĪŖ£ŗ![]() £¬
£¬
B¹¤³Ģ¶ÓÕūÖĪŗÓµĄµÄĆ׏żĪŖ£ŗ![]() .
.
“š£ŗA¹¤³Ģ¶ÓÕūÖĪŗÓµĄ![]() Ć×£¬B¹¤³Ģ¶ÓÕūÖĪŗÓµĄ
Ć×£¬B¹¤³Ģ¶ÓÕūÖĪŗÓµĄ![]() Ć×.
Ć×.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³Åś·¢ŹŠ³”ÓŠÖŠÕŠæ¼ŹŌĪľßĢ××°£¬ĘäÖŠAĘ·ÅʵÄÅś·¢¼ŪŹĒĆæĢ×20ŌŖ£¬BĘ·ÅʵÄÅś·¢¼ŪŹĒĆæĢ×25ŌŖ£¬Š”ĶõŠč¹ŗĀņA”¢BĮ½ÖÖĘ·ÅʵÄĪľßĢ××°¹²1000Ģ×£®
£Ø1£©ČōŠ”Ķõ°“Šč¹ŗĀņA”¢BĮ½ÖÖĘ·ÅĘĪľßĢ××°¹²ÓĆ22000ŌŖ£¬Ōņø÷¹ŗĀņ¶ąÉŁĢ×£æ
£Ø2£©Ę¾»įŌ±æØŌŚ“ĖÅś·¢ŹŠ³”¹ŗĀņÉĢĘ·æÉŅŌ»ńµĆ8ÕŪÓÅ»Ż£¬»įŌ±æØ·ŃÓĆĪŖ500ŌŖ£®ČōŠ”Ķõ¹ŗĀņ»įŌ±æز¢ÓĆ“ĖæØ°“Šč¹ŗĀņ1000Ģ×ĪľßĢ××°£¬¹²ÓĆĮĖyŌŖ£¬ÉčAĘ·ÅĘĪľßĢ××°ĀņĮĖx°ü£¬ĒėĒó³öyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø3£©ČōŠ”Ķõ¹ŗĀņ»įŌ±æز¢ÓĆ“ĖæØ°“Šč¹ŗĀņ1000Ģ×ĪľßĢ××°£¬¹²ÓĆĮĖ20000ŌŖ£¬Ėū¼Ę»®ŌŚĶųµź°üÓŹĻśŹŪÕāĮ½ÖÖĪľßĢ××°£¬ĆæĢ×ĪľßĢ××°Š”ĶõŠčÖ§ø¶ÓŹ·Ń8ŌŖ£¬ČōAĘ·ÅĘĆæĢ×ĻśŹŪ¼Ūøń±ČBĘ·ÅĘÉŁ5ŌŖ£¬ĒėÄć°ļĖū¼ĘĖć£¬AĘ·ÅʵÄĪľßĢ××°ĆæĢ׶ؼŪ²»µĶÓŚ¶ąÉŁŌŖŹ±²Å²»æ÷±¾£ØŌĖĖć½į¹ūČ”ÕūŹż£©£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĻĀĮŠ·½³Ģ£¬ŹōÓŚŅ»ŌŖŅ»“Ī·½³ĢµÄÓŠ£Ø””””£©
¢Łx©2£½![]() £»¢Ś0.5x£½1£»¢Ū
£»¢Ś0.5x£½1£»¢Ū![]() £½8x©1£»¢Üx2©4x£½8£»¢Żx£½0£»¢Žx+2y£½0£®
£½8x©1£»¢Üx2©4x£½8£»¢Żx£½0£»¢Žx+2y£½0£®
A. 5øö B. 4øö C. 3øö D. 2øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,ŅŃÖŖ”ĻAOBŹĒ”ĻAOCµÄÓą½Ē,”ĻAODŹĒ”ĻAOCµÄ²¹½Ē,ĒŅ”ĻBOD=2”ĻBOC,Ēó”ĻBOD”¢”ĻAOCµÄ¶ČŹż.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĪľßÉĢµźĻśŹŪ¹¦ÄÜĻąĶ¬µÄA”¢BĮ½ÖÖĘ·ÅĘµÄ¼ĘĖćĘ÷£¬¹ŗĀņ2øöAĘ·ÅĘŗĶ3øöBĘ·ÅĘµÄ¼ĘĖćĘ÷¹²Šč156ŌŖ£»¹ŗĀņ3øöAĘ·ÅĘŗĶ1øöBĘ·ÅĘµÄ¼ĘĖćĘ÷¹²Šč122ŌŖ£®
£Ø1£©ĒóÕāĮ½ÖÖĘ·ÅĘ¼ĘĖćĘ÷µÄµ„¼Ū£»
£Ø2£©Ń§Š£æŖѧĒ°Ļ¦£¬øĆÉĢµź¶ŌÕāĮ½ÖÖ¼ĘĖćĘ÷æŖÕ¹ĮĖ“ŁĻś»ī¶Æ£¬¾ßĢå°ģ·ØČēĻĀ£ŗAĘ·ÅĘ¼ĘĖćĘ÷°“Ō¼ŪµÄ°ĖÕŪĻśŹŪ£¬BĘ·ÅĘ¼ĘĖćĘ÷5øöŅŌÉĻ³¬³ö²æ·Ö°“Ō¼ŪµÄĘßÕŪĻśŹŪ£¬Éč¹ŗĀņxøöAĘ·ÅĘµÄ¼ĘĖćĘ÷ŠčŅŖy1ŌŖ£¬¹ŗĀņxøöBĘ·ÅĘµÄ¼ĘĖćĘ÷ŠčŅŖy2ŌŖ£¬·Ö±šĒó³öy1”¢y2¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©Š”Ć÷×¼±øĮŖĻµŅ»²æ·ÖĶ¬Ń§¼ÆĢå¹ŗĀņĶ¬Ņ»Ę·ÅĘµÄ¼ĘĖćĘ÷£¬Čō¹ŗĀņ¼ĘĖćĘ÷µÄŹżĮ泬¹ż5øö£¬¹ŗĀņÄÄÖÖĘ·ÅĘµÄ¼ĘĖćĘ÷øüŗĻĖć£æĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻC=90”ć£¬”ĻCAB=50”ć£®°“ŅŌĻĀ²½Öč×÷Ķ¼£ŗ¢ŁŅŌµćAĪŖŌ²ŠÄ£¬Š”ÓŚACµÄ³¤ĪŖ°ė¾¶»»”£¬·Ö±š½»AB”¢ACÓŚµćE”¢F£»¢Ś·Ö±šŅŌµćE”¢FĪŖŌ²ŠÄ£¬“óÓŚ ![]() EFµÄ³¤ĪŖ°ė¾¶»»”£¬Į½»”Ļą½»ÓŚµćG£»¢Ū×÷ÉäĻßAG½»BC±ßÓŚµćD£®Ōņ”ĻADCµÄ¶ČŹżĪŖ £®
EFµÄ³¤ĪŖ°ė¾¶»»”£¬Į½»”Ļą½»ÓŚµćG£»¢Ū×÷ÉäĻßAG½»BC±ßÓŚµćD£®Ōņ”ĻADCµÄ¶ČŹżĪŖ £® 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćA”¢BŌŚ·“±ČĄżŗÆŹży= ![]() £Øk£¾0£¬x£¾0£©µÄĶ¼ĻóÉĻ£¬¹żµćA”¢B×÷xÖįµÄ“¹Ļߣ¬“¹×ć·Ö±šĪŖM”¢N£¬ŃÓ³¤Ļ߶ĪAB½»xÖįÓŚµćC£¬ČōOM=MN=NC£¬”÷AOCµÄĆ껿ĪŖ6£¬ŌņkµÄÖµĪŖ £®
£Øk£¾0£¬x£¾0£©µÄĶ¼ĻóÉĻ£¬¹żµćA”¢B×÷xÖįµÄ“¹Ļߣ¬“¹×ć·Ö±šĪŖM”¢N£¬ŃÓ³¤Ļ߶ĪAB½»xÖįÓŚµćC£¬ČōOM=MN=NC£¬”÷AOCµÄĆ껿ĪŖ6£¬ŌņkµÄÖµĪŖ £® 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÕŪµžČż½ĒŠĪÖ½Ę¬ABC£¬Ź¹µćAĀäŌŚBC±ßÉĻµÄµćF£¬ĒŅÕŪŗŪDE”ĪBC£¬Čō”ĻA=75”ć£¬”ĻC=60”ć£¬Ōņ”ĻBDF=____________________________

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻB=90”ć£¬BC=5 ![]() £¬”ĻC=30”ć£®µćD“ÓµćC³ö·¢ŃŲCA·½ĻņŅŌĆæĆė2øöµ„Ī»³¤µÄĖŁ¶ČĻņµćAŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±µćE“ÓµćA³ö·¢ŃŲAB·½ĻņŅŌĆæĆė1øöµ„Ī»³¤µÄĖŁ¶ČĻņµćBŌČĖŁŌĖ¶Æ£¬µ±ĘäÖŠŅ»øöµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®ÉčµćD”¢EŌĖ¶ÆµÄŹ±¼äŹĒtĆė£Øt£¾0£©£®¹żµćD×÷DF”ĶBCÓŚµćF£¬Į¬½ÓDE”¢EF£®
£¬”ĻC=30”ć£®µćD“ÓµćC³ö·¢ŃŲCA·½ĻņŅŌĆæĆė2øöµ„Ī»³¤µÄĖŁ¶ČĻņµćAŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±µćE“ÓµćA³ö·¢ŃŲAB·½ĻņŅŌĆæĆė1øöµ„Ī»³¤µÄĖŁ¶ČĻņµćBŌČĖŁŌĖ¶Æ£¬µ±ĘäÖŠŅ»øöµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®ÉčµćD”¢EŌĖ¶ÆµÄŹ±¼äŹĒtĆė£Øt£¾0£©£®¹żµćD×÷DF”ĶBCÓŚµćF£¬Į¬½ÓDE”¢EF£® 
£Ø1£©ĒóÖ¤£ŗAE=DF£»
£Ø2£©ĖıߊĪAEFDÄܹ»³ÉĪŖĮāŠĪĀš£æČē¹ūÄÜ£¬Ēó³öĻąÓ¦µÄtÖµ£»Čē¹ū²»ÄÜ£¬ĖµĆ÷ĄķÓÉ£®
£Ø3£©µ±tĪŖŗĪÖµŹ±£¬”÷DEFĪŖÖ±½ĒČż½ĒŠĪ£æĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com