
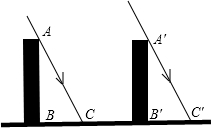
 如图所示,太阳光线AC和A?C?是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?请说明理由.
如图所示,太阳光线AC和A?C?是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?请说明理由. 分析 根据已知同一时刻两个建筑物在太阳下的影子一样长,即可得出BC=B′C′,在直角三角形中,可考虑AAS证明三角形全等,从而推出线段相等.
解答  解:建筑物一样高.
解:建筑物一样高.
证明:∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°,
∵AC∥A′C′,
∴∠ACB=∠A′C′B′,
在△ABC和△A′B′C′中,
$\left\{\begin{array}{l}{∠ABC=∠A′B′C′}\\{BC=B′C′}\\{∠ACB=∠A′C′B′}\end{array}\right.$,
∴△ABC≌△A′B′C′(ASA)
∴AB=A′B′.
即建筑物一样高.
点评 此题考查了全等三角形的应用以及平行投影的性质.在实际生活中,常常通过证明两个三角形得出线段相等.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | y2<0<y1 | B. | y1<0<y2 | C. | y1<y2<0 | D. | y2<y1<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 铁路上A,B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,请画出E点位置(要求尺规作图,保留作图痕迹)并求出E站应建在离A站多少千米处?
铁路上A,B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,请画出E点位置(要求尺规作图,保留作图痕迹)并求出E站应建在离A站多少千米处?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com