
【题目】如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC、∠ABC 之间存在的等量关系是( )

A. ∠AEC=∠ABC﹣2∠ADC B. ∠AEC=![]()
C. ∠AEC= ![]() ∠ABC﹣∠ADC D. ∠AEC=
∠ABC﹣∠ADC D. ∠AEC= ![]()
科目:初中数学 来源: 题型:
【题目】元旦假期,小明一家游览仓圣公园,公园内有一座假山,假山上有一条石阶小路,其中有两段台阶的高度如图所示(图中的数字表示每一级台阶的高度,单位:cm).请你运用所学习的统计知识,解决以下问题:
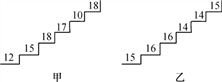
(1)把每一级台阶的高度作为数据,请从统计知识方面(平均数、中位数)说一下甲、乙两段台阶有哪些相同点和不同点?
(2)甲、乙两段台阶哪段上行走会比较舒服?你能用所学知识说明吗?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
解:∵AD∥BC,( )
∴∠ACB+∠DAC=180° ,( )
∵∠DAC=120°,(已知)
∴∠ACB=180°﹣∠DAC= °.
∵∠ACF=20°(已知),
∴∠BCF=∠ACB﹣∠ACF= °.
∵CE平分∠BCF,
∴∠BCE=![]() ∠BCF= °.
∠BCF= °.
∵EF∥AD,AD∥BC,
∴EF∥ ,( )
∴∠FEC=∠BCE= °.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:
①∠A+∠B=∠C
②∠A:∠B:∠C=1:2:3
③∠A= ![]() ∠B=
∠B= ![]() ∠C
∠C
④∠A=∠B=2∠C 中,能确定△ABC 为直角三角形的条件有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,BC=6cm.射线 AG∥BC,点 E 从点 A 出发沿射线 AG 以 2cm/s 的速度运动,当点 E 先出发 1s 后,点 F 也从点 B 出发沿射线 BC 以![]() cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
(1)当 t 为何值时,∠BAF<∠BAC;
(2)当 t 为何值时,AE=CF;
(3)当 t 为何值时,S△ABF+S△ACE<S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳果品店在批发市场购买某种水果销售,第一次用1 200元购进若干千克,并以8元/kg出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1 452元所购买的数量比第一次多20 kg,以9元/kg售出100 kg后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com