
【题目】如图,A(0,2),B(1,0),点C为线段AB的中点,将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)若该抛物线经过原点O,且a=﹣ ![]() ,求该抛物线的解析式;
,求该抛物线的解析式;
(2)在(1)的条件下,点P(m,n)在抛物线上,且∠POB锐角,满足∠POB+∠BCD<90°,求m的取值范围.
【答案】
(1)
解:过点D作DF⊥x轴,垂足为F.

∵∠ABD=90°,
∴∠DBF+∠ABO=90°.
又∵∠OAB+∠ABO=90°,
∴∠DBF=∠OAB.
由旋转的性质可知AB=BD.
在△AOB和△BFD中  ,
,
∴△AOB≌△BFD.
∴DF=OB=1,AO=BF=2.
∴D(3,1).
把点D和点O的坐标代入y=﹣ ![]() x2+bx+c得:
x2+bx+c得: ![]() ,解得:b=
,解得:b= ![]() ,c=0.
,c=0.
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:如图2所示:

∵点A(0,2),B(1,0),C为线段AB的中点,
∴C( ![]() ,1).
,1).
∵C、D两点的纵坐标为1,
∴CD∥x轴.
∴∠BCD=∠ABD.
∴当∠POB=∠BAO时,恰好∠POB+∠BCD=90°.
设点P的坐标为(m,﹣ ![]() m2+
m2+ ![]() m).
m).
当点P在x轴上且∠POB=∠BAO时,则tan∠POB=tan∠BAO= ![]() ,
,
即 ![]() =
= ![]() ,解得:m=
,解得:m= ![]() 或m=0(舍去).
或m=0(舍去).
当点P位于x轴的下方,点P′处时,且∠POB=∠BAO时,则tan∠POB=tan∠BAO= ![]() ,
,
即 ![]() =
= ![]() ,解得:m=
,解得:m= ![]() 或m=0(舍去).
或m=0(舍去).
由图形可知:当点P在抛物线上P与P′之间移动时,∠POB+∠BCD<90°,
∴m的取值范围是: ![]() <m<
<m< ![]()
【解析】(1)过点D作DF⊥x轴,垂足为F.先证明△AOB≌△BFD,于是可得到D(3,1),将a=﹣ ![]() 以及点D和点O的坐标代入抛物线的解析式求解即可;(2)先证明CD∥x轴,依据题意可知:当∠POB=∠BAO时,恰好∠POB+∠BCD=90°,设点P的坐标为(m,﹣
以及点D和点O的坐标代入抛物线的解析式求解即可;(2)先证明CD∥x轴,依据题意可知:当∠POB=∠BAO时,恰好∠POB+∠BCD=90°,设点P的坐标为(m,﹣ ![]() m2+
m2+ ![]() m),由∠POB=∠BAO,可得到tan∠POB=
m),由∠POB=∠BAO,可得到tan∠POB= ![]() ,据此可得到关于m的方程,从而可求得m的值,最后依据图形可得到当∠POB+∠BCD<90°时,m的取值范围.
,据此可得到关于m的方程,从而可求得m的值,最后依据图形可得到当∠POB+∠BCD<90°时,m的取值范围.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


科目:初中数学 来源: 题型:
【题目】海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=8.3海里,DE=30海里,且DE⊥EC,cos∠D= ![]() .
. 
(1)求小岛两端A、B的距离;
(2)过点C作CF⊥AB交AB的延长线于点F,求sin∠BCF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: ![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: ![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() 1.414,
1.414, ![]() 1.732)
1.732)
(1)求点B
距水平面AE的高度BH;
(2)求广告牌CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1、图2、图3分别表示甲、乙、丙三人由甲A地到B地的路线图(箭头表示行进的方向).其中E为AB的中点,AH>HB,判断三人行进路线长度的大小关系为

A.甲<乙<丙 B.乙<丙<甲 C.丙<乙<甲 D.甲=乙=丙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣1),且顶点在第三象限,则a的取值范围是( ) 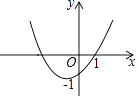
A.a>0
B.0<a<1
C.1<a<2
D.﹣1<a<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20°
B.∠ADE=30°
C.∠ADE=![]() ∠ADC
∠ADC
D.∠ADE=![]() ∠ADC
∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是BD弧上的一点,OE⊥BD于点G,连接AE交BC于点F,AC是⊙O的切线. 
(1)求证:∠ACB=2∠EAB;
(2)若cos∠ACB= ![]() ,AC=10,求BF的长.
,AC=10,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com