
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
【答案】(1)12(2)4(3)存在,16
【解析】
试题分析:(1)首先设点M、N运动x秒后,M、N两点重合,表示出M,N的运动路程,N的运动路程比M的运动路程多12cm,列出方程求解即可;
(2)根据题意设点M、N运动t秒后,可得到等边三角形△AMN,然后表示出AM,AN的长,由于∠A等于60°,所以只要AM=AN三角形ANM就是等边三角形;
(3)首先假设△AMN是等腰三角形,可证出△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB,NM的长,列出方程,可解出未知数的值.
试题解析:(1)设点M、N运动x秒后,M、N两点重合,
x×1+12=2x,解得:x=12;
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB-BN=12-2t,∵三角形△AMN是等边三角形,∴t=12-2t,
解得t=4,∴点M、N运动4秒后,可得到等边三角形△AMN.

(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知12秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,∴AN=AM,∴∠AMN=∠ANM,
∴∠AMC=∠ANB,∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,
在△ACM和△ABN中,
∵ ,∴△ACM≌△ABN,∴CM=BN,
,∴△ACM≌△ABN,∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y-12,NB=36-2y,CM=NB,y-12=36-2y,解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.


科目:初中数学 来源: 题型:
【题目】2015年9月24日台风杜鹃登陆,给我福建、浙江等地造成严重影响.为民排忧解难的解放军叔叔驾着冲锋舟沿一条东西方向的河流营救灾民,早晨从A地出发,晚上最后到达B地,约定向东为正方向,当天航行依次记录如下(单位:千米):
14,﹣9,18,﹣7,13,﹣6,10,﹣5
问:(1)B地在A地的东面,还是西面?与A地相距多少千米?
(2)这一天冲锋舟离A地最远多少千米?
(3)若冲锋舟每千米耗油0.5升,油箱容量为30升,求途中至少需要补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从少年宫出发,沿相同的路分别以不同的速度匀速跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超出甲150米时,乙停在此地等候甲,两人相遇后乙又继续以原来的速度跑向体育馆.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象.
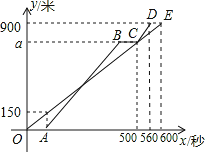
(1)在跑步的全过程中,甲共跑了 米, 甲的速度为 米/秒;
(2)乙跑步的速度是多少?乙在途中等候甲用了多长时间?
(3)甲出发多长时间第一次与乙相遇?此时乙跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面有8个算式,排成4行2列
2+2, 2×2
3+![]() , 3×
, 3×![]()
4+![]() , 4×
, 4×![]()
5+![]() , 5×
, 5×![]()
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+![]() 和2005×
和2005×![]() 的结果相等吗?
的结果相等吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() 交x轴于点A、B,交y轴于点C,点A的坐标是(-1,0),点C的坐标是(0,2).
交x轴于点A、B,交y轴于点C,点A的坐标是(-1,0),点C的坐标是(0,2).
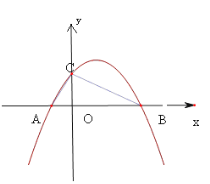
(1)求该抛物线的解析式。
(2)已知点P是抛物线上的一个动点,点N在x轴上。
①若点P在x轴上方,且△APN是等腰直角三角形,求点N的坐标;
②若点P在x轴下方,且△APN∽△BOC,请直接写出点N的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com