
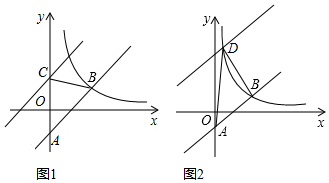
·ÖĪö £Ø1£©ĻČøł¾ŻÖ±Ļßy=2x-1¾¹żµćB£Øm£¬2£©£¬ĒóµĆB£Ø1.5£¬2£©£¬ŌŁøł¾Ż·“±ČĄżŗÆŹży=$\frac{k}{x}$£Øx£¾0£©µÄĶ¼Ļó¾¹żµćB£¬¼“æɵƵ½kµÄÖµ£»
£Ø2£©¹żB×÷BH”ĶyÖįÓŚH£¬øł¾ŻAC=4£¬BH=1.5£¬¼“æɵƵ½”÷ABCµÄĆ껿£»
£Ø3£©ÉčÖ±Ļßy=2x-1ĻņÉĻĘ½ŅĘŗóÓėyÖį½»ÓŚµćE£¬Į¬½ÓBE£¬¹żB×÷BM”ĶyÖįÓŚM£¬ŌņBM=1.5£¬øł¾ŻDE”ĪAB£¬æɵĆS”÷ABE=S”÷ABD=3£¬½ų¶ųµĆµ½AE=4£¬ŌŁøł¾ŻOA=1£¬æɵĆOE=3£¬¼“æÉµĆ³öĘ½ŅĘŗóÖ±Ļߵıķ“ļŹ½ĪŖy=2x+3£®
½ā“š 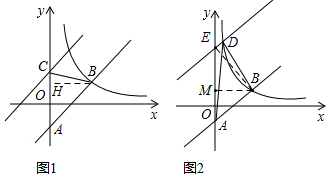 ½ā£ŗ£Ø1£©”ßÖ±Ļßy=2x-1¾¹żµćB£Øm£¬2£©£¬
½ā£ŗ£Ø1£©”ßÖ±Ļßy=2x-1¾¹żµćB£Øm£¬2£©£¬
”ą2=2m-1£¬
½āµĆm=1.5£¬
”ąB£Ø1.5£¬2£©£¬
”ß·“±ČĄżŗÆŹży=$\frac{k}{x}$£Øx£¾0£©µÄĶ¼Ļó¾¹żµćB£¬
”ąk=1.5”Į2=3£¬
”ą·“±ČĄżŗÆŹżµÄ±ķ“ļŹ½ĪŖy=$\frac{3}{x}$£»
£Ø2£©ČēĶ¼1£¬¹żB×÷BH”ĶyÖįÓŚH£¬
ÓÉĘ½ŅĘæÉµĆ£¬AC=4£¬
ÓÖ”ßB£Ø1.5£¬2£©£¬
”ąBH=1.5£¬
”ą”÷ABCµÄĆ껿=$\frac{1}{2}$”Į4”Į1.5=3£¬
¼“”÷ABCµÄĆ껿ĪŖ3£»
£Ø3£©ČēĶ¼2£¬ÉčÖ±Ļßy=2x-1ĻņÉĻĘ½ŅĘŗóÓėyÖį½»ÓŚµćE£¬Į¬½ÓBE£¬¹żB×÷BM”ĶyÖįÓŚM£¬ŌņBM=1.5£¬
”ßDE”ĪAB£¬”÷ABDµÄĆ껿ĪŖ3£¬
”ąS”÷ABE=S”÷ABD=3£¬
”ą$\frac{1}{2}$AE”ĮBM=3£¬¼“$\frac{1}{2}$”ĮAE”Į1.5=3£¬
½āµĆAE=4£¬
”ßÖ±Ļßy=2x-1ÓėyÖįĻą½»ÓŚµćA£Ø0£¬-1£©£¬
”ąOA=1£¬
”ąOE=3£¬
”ąĘ½ŅĘŗóÖ±Ļߵıķ“ļŹ½ĪŖy=2x+3£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²éĮĖ·“±ČĄżŗÆŹżÓėŅ»“ĪŗÆŹż½»µćĪŹĢāŅŌ¼°Čż½ĒŠĪĆ껿¼ĘĖćĪŹĢā£¬½āĢāŹ±×¢Ņā£ŗ·“±ČĄżŗÆŹżÓėŅ»“ĪŗÆŹżµÄ½»µć×ų±źĶ¬Ź±Āś×ć·“±ČĄżŗÆŹżÓėŅ»“ĪŗÆŹżµÄ½āĪöŹ½£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬Õż·½ŠĪABCDµÄĆ껿ĪŖ1£®”÷BPCĪŖµČ±ßČż½ĒŠĪ£®Ōņ”÷PBDµÄĆ껿ĪŖ$\frac{\sqrt{3}-1}{4}$£®
ČēĶ¼£¬Õż·½ŠĪABCDµÄĆ껿ĪŖ1£®”÷BPCĪŖµČ±ßČż½ĒŠĪ£®Ōņ”÷PBDµÄĆ껿ĪŖ$\frac{\sqrt{3}-1}{4}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -1 | B£® | 0 | C£® | 1 | D£® | 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
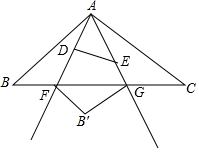 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC=4£¬”ĻBAC=90”ć£¬ŅŌAĪŖŅ»øö¶„µćµÄµČŃüRt”÷ADE£¬”ĻADE=90”ć£¬ČʵćAŌŚ”ĻBACÄŚŠż×Ŗ£¬AD”¢AEĖłŌŚµÄÖ±ĻßÓėBC±ß·Ö±š½»ÓŚµćF”¢G£¬ČōµćB¹ŲÓŚÖ±ĻßADµÄ¶Ō³ĘµćĪŖB”䣬µ±”ĻCFB”ä=60”揱£¬ŌņBFµÄ³¤ĪŖ$\frac{6\sqrt{2}-2\sqrt{3}}{3}$£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC=4£¬”ĻBAC=90”ć£¬ŅŌAĪŖŅ»øö¶„µćµÄµČŃüRt”÷ADE£¬”ĻADE=90”ć£¬ČʵćAŌŚ”ĻBACÄŚŠż×Ŗ£¬AD”¢AEĖłŌŚµÄÖ±ĻßÓėBC±ß·Ö±š½»ÓŚµćF”¢G£¬ČōµćB¹ŲÓŚÖ±ĻßADµÄ¶Ō³ĘµćĪŖB”䣬µ±”ĻCFB”ä=60”揱£¬ŌņBFµÄ³¤ĪŖ$\frac{6\sqrt{2}-2\sqrt{3}}{3}$£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com