
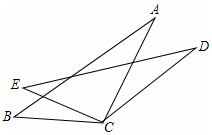
 如图,AC=DC,BE=EC,∠BCE=∠ACD.求证:∠A=∠D.
如图,AC=DC,BE=EC,∠BCE=∠ACD.求证:∠A=∠D.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.
如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD于E,交直线AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
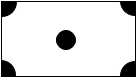 如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,正中设计一个圆形喷水池,若四周圆形和中间圆形的半径均为r米,广场长为a米,宽为b米.
如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,正中设计一个圆形喷水池,若四周圆形和中间圆形的半径均为r米,广场长为a米,宽为b米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 都扩大到原来的2倍 | B. | 都缩小到原来的一半 | ||
| C. | 没有变化 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
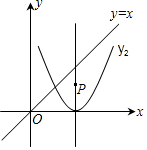 如图,P是抛物线y=2(x-2)2的对称轴上一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,则满足条件的t值有( )
如图,P是抛物线y=2(x-2)2的对称轴上一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,则满足条件的t值有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com