
【题目】如图,在![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,有下列条件:
上,有下列条件:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中,能使四边形
.其中,能使四边形![]() 是平行四边形的条件有( ).
是平行四边形的条件有( ).

A.1个B.2个C.3个D.4个
【答案】C
【解析】
在ABCD中,AD=BC,AD∥BC,又BE=DF,得出AF=EC,即可得出四边形AECF是平行四边形,①正确;由AF∥EC,AE∥CF,得出四边形AECF是平行四边形,②正确;由平行四边形的性质和∠BAE=∠DCF证出AE∥CF,得出四边形AECF是平行四边形,④正确;③不正确;即可得出结果.
①正确,理由如下:
∵四边形ABCD平行四边形,
∴AD=BC,AD∥BC,
又∵BE=DF,
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
②正确,理由如下:
∵AF∥EC,AE∥CF,
∴四边形AECF是平行四边形;
④正确;理由如下:
∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵∠BAE=∠DCF,
∴∠AEB=∠CFD.
∵AD∥BC,
∴∠AEB=∠EAD.
∴∠CFD=∠EAD.
∴AE∥CF.
∵AF∥CE,
∴四边形AECF是平行四边形.
∵AE=CF不能得出四边形AECF是平行四边形,
∴③不正确;
能使四边形AECF是平行四边形的条件有3个.
故选:C.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】下面是“作一个角等于30°”的尺规作图过程.
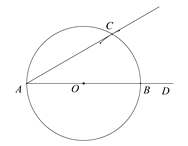
作法:如图,(1)作射线AD;
(2)在射线AD上任意取一点O(点O不与点A重合);
(3)以点O为圆心,OA为半径作⊙O,交射线AD于点B;
(4)以点B为圆心,OB为半径作弧,交⊙O于点C;
(5)作射线AC.
∠DAC即为所求作的30°角.
请回答:该尺规作图的依据是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是以AB为直径的⊙O上一动点,过点C作⊙O直径CD,过点B作BE⊥CD于点E.已知AB=6cm,设弦AC的长为xcm,B,E两点间的距离为ycm(当点C与点A或点B重合时,y的值为0).
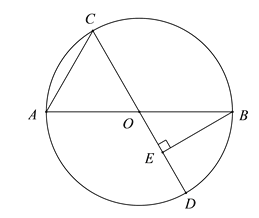
小冬根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小冬的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
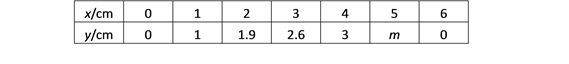
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)在(2)的条件下,当函数图象与直线![]() 相交时(原点除外),∠BAC的度数是_____.
相交时(原点除外),∠BAC的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的顶点为点D.
的顶点为点D.
(1)求点D的坐标(用含m的代数式表示);
(2)求函数![]() 的图象与x轴的交点坐标;
的图象与x轴的交点坐标;
(3)若函数![]() 的图象在直线y=m的上方,求m的取值范围.
的图象在直线y=m的上方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
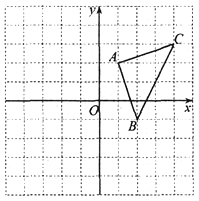
【题目】如图,平面直角坐标系中,△ABC的顶点坐标为:A(1,2),B(2, 一1), C (4, 3).
(1)将△ABC向左平移2个单位长度,再向上平移1个单位长度,得△A'B'C'.画出△A'B'C',并写出△A'B'C'的顶点坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )

A. 从D点出发,沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发,沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发,沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发,沿线段CN→弧ND→弧DA→线段AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为BC中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF、AF、AD,AD与CF交于点G.
(1)求证:△ACD≌△CBF;
(2)AD与CF的关系是 ;
(3)求证:△ACF是等腰三角形;
(4)△ACF可能是等边三角形吗? (填“可能”或“不可能”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题一:如图1,已知A,C两点之间的距离为16 cm,甲,乙两点分别从相距3cm的A,B两点同时出发到C点,若甲的速度为8 cm/s,乙的速度为6 cm/s,设乙运动时间为x(s), 甲乙两点之间距离为y(cm).
(1)当甲追上乙时,x = .
(2)请用含x的代数式表示y.
当甲追上乙前,y= ;
当甲追上乙后,甲到达C之前,y= ;
当甲到达C之后,乙到达C之前,y= .
![]()
问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动 cm;时针OE指向圆周上的点的速度为每分钟转动 cm.
(2)若从4:00起计时,求几分钟后分针与时针第一次重合.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com