
【题目】已知点O是坐标原点,反比例函数y=![]() 的图像经过A(
的图像经过A(![]() ,1).
,1).
(1)求此反比例函数的解析式;
(2)将线段OA绕O逆时针旋转30°得到线段OB,判断点B是否在此反比例函数的图像上并说明理由.
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+m)2的顶点坐标为(﹣1,0),且过点A(﹣2,﹣![]() ).
).
(1)求这个二次函数的解析式;
(2)点B(2,﹣2)在这个函数图象上吗?
(3)你能通过左,右平移函数图象,使它过点B吗?若能,请写出平移方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师所留的作业中有这样一个分式的计算题:![]() ,甲、乙两位同学完成的过程分别如下:
,甲、乙两位同学完成的过程分别如下:
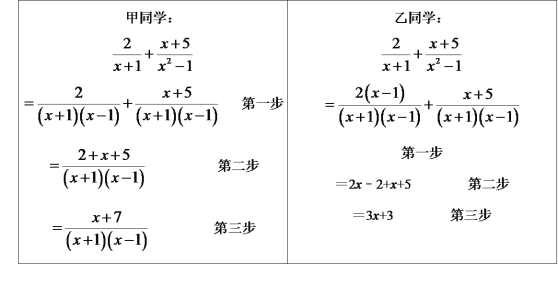
老师发现这两位同学的解答都有错误.
请你从甲、乙两位同学中,选择一位同学的解答过程,帮助他分析错因,并加以改正.
(1)我选择 同学的解答过程进行分析.(填“甲”或“乙”)该同学的解答从第 步开始出现错误,错误的原因是 ;
(2)请重新写出完成此题的正确解答过程.
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知二次函数![]() 的图象经过点(﹣2,8)和(﹣1,5),求这个二次函数的表达式;
的图象经过点(﹣2,8)和(﹣1,5),求这个二次函数的表达式;
(2)已知抛物线的顶点为(﹣1,﹣3),与y轴的交点为(0,﹣5),求这个抛物线相应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为![]() ,格点三角形(顶点是网格线的交点的三角形)
,格点三角形(顶点是网格线的交点的三角形)![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
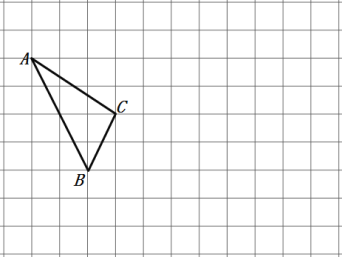
(1)请在如图所示的网格内作出![]() 轴、
轴、![]() 轴;
轴;
(2)请作出![]() 关于
关于![]() 轴对称的
轴对称的![]() (不写画法),并写出点
(不写画法),并写出点![]() 的坐标;
的坐标;
(3)求出![]() 关于
关于![]() 轴对称的
轴对称的![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,点Q坐标为(x,y),若过点Q的直线l与x轴夹角为45°时,则称直线l为点Q的“湘依直线”.
(1)已知点A的坐标为(6,0),求点A的“湘依直线”表达式;
(2)已知点D的坐标为(0,﹣4),过点D的“湘依直线”图象经过第二、三、四象限,且与x轴交于C点,动点P在反比例函数y=![]() (x>0)上,求△PCD面积的最小值及此时点P的坐标;
(x>0)上,求△PCD面积的最小值及此时点P的坐标;
(3)已知点M的坐标为(0,2),经过点M且在第一、二、三象限的“湘依直线”与抛物线y=x2+(m﹣2)x+m+2相交与A(x1,y1),B(x2,y2)两点,若0≤x1≤2,0≤x2≤2,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com