
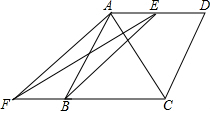
 如图,在菱形ABCD中,E是AD的中点,EF⊥AC交CB的延长线于点F,连接AF,BE.
如图,在菱形ABCD中,E是AD的中点,EF⊥AC交CB的延长线于点F,连接AF,BE.分析 (1)设AB、EF相交于G,连接BD,根据菱形的对角线互相垂直可得BD⊥AC,然后求出EG∥BD,判断出EG是△ABD的中位线,从而求出AG=BG,再根据两直线平行,内错角相等求出∠AEG=∠BFG,利用“角角边”证明△AEG和△BFG全等,根据全等三角形对应边相等可得AE=BF,从而求出DE=BF;
(2)根据一组对边平行且相等是四边形是平行四边形解答.
解答  解:(1)DE=BF.
解:(1)DE=BF.
理由如下:如图,设AB、EF相交于G,连接BD,
在菱形ABCD中,BD⊥AC,
∵EF⊥AC,
∴EG∥BD,
∵E是AD中点,
∴EG是△ABD的中位线,
∴AG=BG,
又∵AD∥BC,
∴∠AEG=∠BFG,
在△AEG和△BFG中,
$\left\{\begin{array}{l}{∠AEG=∠BFG}\\{∠AGE=∠BGF}\\{AG=BG}\end{array}\right.$,
∴△AEG≌△BFG(AAS),
∴AE=BF,
∵E是AD中点,
∴AE=DE,
∴DE=BF;
(2)四边形AFBE是平行四边形.
理由如下:∵四边形ABCD是菱形,
∴AD∥BC,
∴AE∥BF,
又∵AE=BF,
∴四边形AFBE是平行四边形.
点评 本题考查了菱形的性质,平行四边形的判定,全等三角形的判定与性质,主要利用了菱形的对角线互相垂直的性质,作辅助线构造出全等三角形的是解题的关键,也是本题的难点.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩 | 66 | 90 | 86 | 64 | 66 | 84 |
| 专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
| 说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
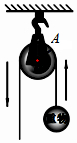 一个滑轮起重装置如图所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时,重物上升$\frac{20}{3}$πcm(结果保留π).
一个滑轮起重装置如图所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时,重物上升$\frac{20}{3}$πcm(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由-2y-5=-1+y,得-2y-y=5-1 | B. | 由-3x=-6,得x=2 | ||
| C. | 由$\frac{1}{5}$y=2,得y=10 | D. | 由-2(1-2x)+3=0,得-2+4x+3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com