
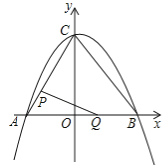
ЁОЬтФПЁПШчЭМЂйЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃН![]() x2+bx+cЕФЭМЯѓгызјБъжсНЛгкAЃЌBЃЌCШ§ЕуЃЌЦфжаЕуAЕФзјБъЮЊЃЈЉ3ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЌСЌНгACЃЌBCЃЎЖЏЕуPДгЕуAГіЗЂЃЌдкЯпЖЮACЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуCзїдШЫйдЫЖЏЃЛЭЌЪБЃЌЖЏЕуQДгЕуOГіЗЂЃЌдкЯпЖЮOBЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуBзїдШЫйдЫЖЏЃЌЕБЦфжавЛЕуЕНДяжеЕуЪБЃЌСэвЛЕуЫцжЎЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎСЌНгPQЃЎ
x2+bx+cЕФЭМЯѓгызјБъжсНЛгкAЃЌBЃЌCШ§ЕуЃЌЦфжаЕуAЕФзјБъЮЊЃЈЉ3ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЌСЌНгACЃЌBCЃЎЖЏЕуPДгЕуAГіЗЂЃЌдкЯпЖЮACЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуCзїдШЫйдЫЖЏЃЛЭЌЪБЃЌЖЏЕуQДгЕуOГіЗЂЃЌдкЯпЖЮOBЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуBзїдШЫйдЫЖЏЃЌЕБЦфжавЛЕуЕНДяжеЕуЪБЃЌСэвЛЕуЫцжЎЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎСЌНгPQЃЎ
ЃЈ1ЃЉЬюПеЃКbЃН ЃЌcЃН ЃЛ
ЃЈ2ЃЉдкЕуPЃЌQдЫЖЏЙ§ГЬжаЃЌЁїAPQПЩФмЪЧжБНЧШ§НЧаЮТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуMдкХзЮяЯпЩЯЃЌЧвЁїAOMЕФУцЛ§гыЁїAOCЕФУцЛ§ЯрЕШЃЌЧѓГіЕуMЕФзјБъЁЃ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ4ЃЛЃЈ2ЃЉВЛПЩФмЪЧжБНЧШ§НЧаЮЃЌМћНтЮіЃЛЃЈ3ЃЉM(1,4)ЛђM(
ЃЌ4ЃЛЃЈ2ЃЉВЛПЩФмЪЧжБНЧШ§НЧаЮЃЌМћНтЮіЃЛЃЈ3ЃЉM(1,4)ЛђM(![]() ,-4ЃЉЛђM(
,-4ЃЉЛђM(![]() ,-4ЃЉ
,-4ЃЉ
ЁОНтЮіЁП
(1)ЩшХзЮяЯпЕФНтЮіЪНЮЊy=aЃЈx+3ЃЉЃЈx-4ЃЉЃЎНЋa=-![]() ДњШыПЩЕУЕНХзЮяЯпЕФНтЮіЪНЃЌДгЖјПЩШЗЖЈГіbЁЂcЕФжЕЃЛ
ДњШыПЩЕУЕНХзЮяЯпЕФНтЮіЪНЃЌДгЖјПЩШЗЖЈГіbЁЂcЕФжЕЃЛ
ЃЈ2ЃЉЯШЧѓЕУЕуCЕФзјБъЃЌвРОнЙДЙЩЖЈРэПЩЧѓЕУAC=5ЃЌдђPC=5-tЃЌAQ=3+t,дйХаЖЯЕБЁїAPQЪЧжБНЧШ§НЧаЮЪБЃЌдђЁЯAPQЃН90ЁуЃЌДгЖјЕУГі![]() AOC
AOC![]() APQЃЌЕУЕНБШР§ЪНСаЗНГЬЧѓНтМДПЩЃЛ
APQЃЌЕУЕНБШР§ЪНСаЗНГЬЧѓНтМДПЩЃЛ
(3)ИљОнЕуMдкХзЮяЯпЩЯЃЌЩшГіЕуMЕФзјБъЮЊЃЈmЃЌЉ![]() m2+
m2+![]() m+4ЃЉЃЌдйИљОнЁїAOMЕФУцЛ§гыЁїAOCЕФУцЛ§ЯрЕШЃЌДгЖјЕУГіЉ
m+4ЃЉЃЌдйИљОнЁїAOMЕФУцЛ§гыЁїAOCЕФУцЛ§ЯрЕШЃЌДгЖјЕУГіЉ![]() m2+
m2+![]() m+4=
m+4=![]() ЃЌНтЗНГЬМДПЩЃЎ
ЃЌНтЗНГЬМДПЩЃЎ
НтЃКЃЈ1ЃЉЩшХзЮяЯпЕФНтЮіЪНЮЊyЃНaЃЈx+3ЃЉЃЈxЉ4ЃЉЃЎНЋaЃНЉ![]() ДњШыЕУЃКyЃНЉ
ДњШыЕУЃКyЃНЉ![]() x2+
x2+![]() x+4ЃЌ
x+4ЃЌ
ЁрbЃН![]() ЃЌcЃН4ЃЎ
ЃЌcЃН4ЃЎ
ЃЈ2ЃЉдкЕуPЁЂQдЫЖЏЙ§ГЬжаЃЌЁїAPQВЛПЩФмЪЧжБНЧШ§НЧаЮЃЎ
РэгЩШчЯТЃКЁпдкЕуPЁЂQдЫЖЏЙ§ГЬжаЃЌЁЯPAQЁЂЁЯPQAЪМжеЮЊШёНЧЃЌ
ЁрЕБЁїAPQЪЧжБНЧШ§НЧаЮЪБЃЌдђЁЯAPQЃН90ЁуЃЎ
НЋxЃН0ДњШыХзЮяЯпЕФНтЮіЪНЕУЃКyЃН4ЃЌ
ЁрCЃЈ0ЃЌ4ЃЉЃЎЁпЕуAЕФзјБъЮЊЃЈЉ3ЃЌ0ЃЉЃЌ
ЁрдкRtЁїAOCжаЃЌвРОнЙДЙЩЖЈРэЕУЃКACЃН5ЃЌ
ЁпAPЃНOQЃНtЃЌЁрAQ=3+tЃЌ
ЁпЁЯOACЃНЁЯPAQЃЌЁЯAPQЃНЁЯAOC
Ёр![]() AOC
AOC![]() APQ
APQ
ЁрAP:AO=AQ:AC
Ёр![]() =
=![]() Ёрt=4.5ЃЎ
Ёрt=4.5ЃЎ
ЁпгЩЬтвтПЩжЊЃК0ЁмtЁм4ЃЌ
ЁрtЃН4.5ВЛКЯЬтвтЃЌМДЁїAPQВЛПЩФмЪЧжБНЧШ§НЧаЮЃЎ
(3 )ЩшЕуMЕФзјБъЮЊЃЈmЃЌЉ![]() m2+
m2+![]() m+4ЃЉ
m+4ЃЉ
ЁпЁїAOMЕФУцЛ§гыЁїAOCЕФУцЛ§ЯрЕШЃЌЧвЕзЖМЮЊAOЃЌCЃЈ0ЃЌ4ЃЉЃЎ
ЁрЉ![]() m2+
m2+![]() m+4=
m+4=![]()
ЕБЉ![]() m2+
m2+![]() m+4=-4ЪБЃЌНтЕУЃКm=
m+4=-4ЪБЃЌНтЕУЃКm=![]() Лђ
Лђ![]() ,
,
ЕБЉ![]() m2+
m2+![]() m+4=4ЪБЃЌНтЕУЃКm=1Лђ0
m+4=4ЪБЃЌНтЕУЃКm=1Лђ0
ЁпЕБm=0ЪБЃЌгыCжиКЯЃЌЁрm=![]() Лђ
Лђ![]() Лђ1
Лђ1
Ёр M(1,4)ЛђM(![]() ,-4ЃЉЛђM(
,-4ЃЉЛђM(![]() ,-4ЃЉ
,-4ЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
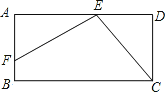
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮABCDжаЃЌEЪЧADЩЯвЛЕуЃЌFЪЧABЩЯЕФвЛЕуЃЌEFЁЭECЃЌЧвEF=ECЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAEFЁеЁїDCEЃЎ
ЃЈ2ЃЉШєDE=4cmЃЌОиаЮABCDЕФжмГЄЮЊ32cmЃЌЧѓAEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
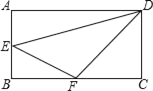
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮABCDжаЃЌABЃН4cmЃЌBCЃН8cmЃЎEЁЂFЗжБ№ЪЧABЁЂBCЕФжаЕуЃЎдђEЕНDFЕФОрРыЪЧ_____cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЙКНјвЛХњЕЅМлЮЊ4дЊЕФШегУЦЗЃЌШєАДУПМў5дЊЕФМлИёЯњЪлЃЌУПЬьФмТєГі300МўЃЌШєАДУПМў6дЊЕФМлИёЯњЪлЃЌУПЬьФмТєГі200МўЃЌМйЖЈУПЬьЯњЪлМўЪ§![]() ЃЈМўЃЉгыМлИё
ЃЈМўЃЉгыМлИё![]() ЃЈдЊ/МўЃЉжЎМфТњзувЛДЮКЏЪ§ЙиЯЕЃЎ
ЃЈдЊ/МўЃЉжЎМфТњзувЛДЮКЏЪ§ЙиЯЕЃЎ
ЃЈ1ЃЉЪдЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉСюУПЬьЕФРћШѓЮЊ![]() ЃЌЧѓГі
ЃЌЧѓГі![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛЕБЯњЪлМлИёЖЈЮЊЖрЩйЪБЃЌВХФмЪЙУПЬьЕФРћШѓзюДѓЃПУПЬьзюДѓРћШѓЪЧЖрЩйЃП
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛЕБЯњЪлМлИёЖЈЮЊЖрЩйЪБЃЌВХФмЪЙУПЬьЕФРћШѓзюДѓЃПУПЬьзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAЃЌBСНЕиБЛДѓЩНзшИєЃЌШєвЊДгAЕиЕНBЕиЃЌжЛФмбизХШчЭМЫљЪОЕФЙЋТЗЯШДгAЕиЕНCЕиЃЌдйгЩCЕиЕНBЕиЃЎЯжМЦЛЎПЊдфЫэЕРAЃЌBСНЕижБЯпЙсЭЈЃЌОВтСПЕУЃКЁЯCAB=30ЁуЃЌЁЯCBA=45ЁуЃЌAC=20kmЃЌЧѓЫэЕРПЊЭЈКѓгыЫэЕРПЊЭЈЧАЯрБШЃЌДгAЕиЕНBЕиЕФТЗГЬНЋЫѕЖЬЖрЩйЃПЃЈНсЙћОЋШЗЕН0.1kmЃЌВЮПМЪ§ОнЃК ![]() Ёж1.414ЃЌ
Ёж1.414ЃЌ ![]() Ёж1.732ЃЉ
Ёж1.732ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊA(Љ4ЃЌa)ЃЌB(Љ1ЃЌ2)ЪЧвЛДЮКЏЪ§y1=kx+bгыЗДБШР§КЏЪ§y2=![]() (mЃМ0)ЭМЯѓЕФСНИіНЛЕуЃЌACЁЭxжсгкCЃЎ
(mЃМ0)ЭМЯѓЕФСНИіНЛЕуЃЌACЁЭxжсгкCЃЎ

(1)ЧѓГіkЃЌbМАmЕФжЕЃЎ
(2)ИљОнЭМЯѓжБНгЛиД№ЃКдкЕкЖўЯѓЯоФкЃЌЕБy1ЃОy2ЪБЃЌxЕФШЁжЕЗЖЮЇЪЧ ________ЃЎ
(3)ШєPЪЧЯпЖЮABЩЯЕФвЛЕуЃЌСЌНгPCЃЌШєЁїPCAЕФУцЛ§ЕШгк![]() ЃЌЧѓЕуPзјБъЃЎ
ЃЌЧѓЕуPзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЪЧдВOЕФЧаЯпЃЌЧаЕуЮЊAЃЌABЪЧдВOЕФЯвЁЃЙ§ЕуBзїBC//ADЃЌНЛдВOгкЕуCЃЌСЌНгACЃЌЙ§ЕуCзїCD//ABЃЌНЛADгкЕуDЁЃСЌНгAOВЂбгГЄНЛBCгкЕуMЃЌНЛЙ§ЕуCЕФжБЯпгкЕуPЃЌЧвBCP=ACDЁЃ
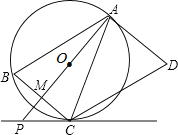
ЃЈ1ЃЉХаЖЯжБЯпPCгыдВOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃК
ЃЈ2ЃЉ ШєAB=9ЃЌBC=6ЃЌЧѓPCЕФГЄЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁзМБИНјвЛХњСНжжВЛЭЌаЭКХЕФвТЗўЃЌвбжЊЙКНјAжжаЭКХвТЗў9МўЃЌBжжаЭКХвТЗў10МўЃЌдђЙВаш1810дЊЃЛШєЙКНјAжжаЭКХвТЗў12МўЃЌBжжаЭКХвТЗў8МўЃЌЙВаш1880дЊЃЛвбжЊЯњЪлвЛМўAаЭКХвТЗўПЩЛёРћ18дЊЃЌЯњЪлвЛМўBаЭКХвТЗўПЩЛёРћ30дЊЃЌвЊЪЙдкетДЮЯњЪлжаЛёРћВЛЩйгк699дЊЃЌЧвAаЭКХвТЗўВЛЖргк28МўЃЎ
ЃЈ1ЃЉЧѓAЁЂBаЭКХвТЗўНјМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉШєвбжЊЙКНјAаЭКХвТЗўЪЧBаЭКХвТЗўЕФ2БЖЛЙЖр4МўЃЌдђЩЬЕъдкетДЮНјЛѕжаПЩгаМИжжЗНАИВЂМђЪіЙКЛѕЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁвЛжжЩЬЦЗЕФНјМлЮЊУПМў30дЊЃЌЪлМлЮЊУПМў40дЊЃЎУПЬьПЩвдЯњЪл48МўЃЌЮЊОЁПьМѕЩйПтДцЃЌЩЬГЁОіЖЈНЕМлДйЯњЃЎ
ЃЈ1ЃЉШєИУЩЬЦЗСЌајСНДЮЯТЕїЯрЭЌЕФАйЗжТЪКѓЪлМлНЕжСУПМў32.4дЊЃЌЧѓСНДЮЯТНЕЕФАйЗжТЪЃЛ
ЃЈ2ЃЉОЕїВщЃЌШєУПНЕМл0.5дЊЃЌУПЬьПЩЖрЯњЪл4МўЃЌФЧУДУПЬьвЊЯыЛёЕУ510дЊЕФРћШѓЃЌУПМўгІНЕМлЖрЩйдЊЃП

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com