
| 车型 | 载货能力(箱/辆) | 运费 | |
| 甲村(元/辆) | 乙村(元/辆) | ||
| 大货车 | 70 | 800 | 900 |
| 小货车 | 35 | 400 | 600 |
分析 (1)根据题意和表格中的数据可以列出相应的方程组,从而可以解答本题;
(2)根据题意和表格中的数据可以用含x的代数式表示出y,进而写出自变量x的取值范围;
(3)根据运往甲村的鱼苗不少于980箱和(2)中的函数解析式可以求得x的取值范围,从而可以求得y的最小值,本题得以解决.
解答 解:(1)设大货车用x辆,小货车用y辆,
$\left\{\begin{array}{l}{x+y=20}\\{70x+35y=1225}\end{array}\right.$,得$\left\{\begin{array}{l}{x=15}\\{y=5}\end{array}\right.$,
答:大货车用15辆,小货车用5辆;
(2)由题意可得,
y=800x+900(15-x)+400(16-x)+600[5-(16-x)]=100x+13300(11≤x≤15且x为整数),
即y与x的函数解析式是:y=100x+13300(11≤x≤15且x为整数);
(3)由题意可得,
70x+35(16-x)≥980,
解得,x≥12,
又∵11≤x≤15且x为整数,
∴12≤x≤15且x为整数,
∵y=100x+13300,
∴当x=12时,y取得最小值,此时y=14500,
答:总费用最少的货车调配方案是12辆大货车、4辆小货车前往甲村,3辆大货车、1辆小货车前往乙村,最少费用为14500元.
点评 本题考查一次函数的应用、二元一次方程组的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
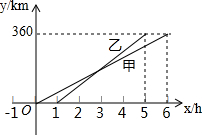 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,两人行驶的路程y(km)与甲出发的时间x(h)之间的函数图象如图所示.根据图象得到如下结论,其中错误的是( )
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,两人行驶的路程y(km)与甲出发的时间x(h)之间的函数图象如图所示.根据图象得到如下结论,其中错误的是( )| A. | 甲的速度是60km/h | B. | 乙比甲早1小时到达 | ||
| C. | 乙出发3小时追上甲 | D. | 乙在AB的中点处追上甲 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
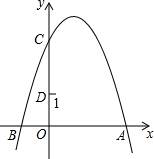 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
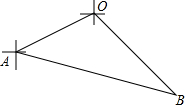 如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为10+10$\sqrt{3}$海里/小时?
如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为10+10$\sqrt{3}$海里/小时?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
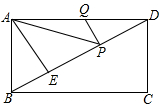 如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com