练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算或因式分【解析】
    (1)计算：(a2－4)÷；(2)因式分【解析】
    a(n－1)2－2a(n－1)＋a.

    （1）原式＝a2－2a；（2）原式＝a(n－2)2. 【解析】试题分析：（1）先把括号内的进行因式分解，然后把除法转化成乘法进行约分即可得解； （2）首先提取公因式a，再利用完全平方公式分解因式得出答案. 试题解析：(1)原式＝(a＋2)(a－2) ＝a(a－2)＝a2－2a； (2)原式＝a[(n－1)2－2(n－1)＋1]＝a(n－1－1)2＝a(n－2)2. ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年黑龙江省哈尔滨市双城区七年级（上）期末数学试卷（五四学制） 题型：填空题

    如图，∠AOB=90°，以O为顶点的锐角共有 个

    5 【解析】 试题分析：根据题意可得锐角为：∠BOC、∠BOD、∠COD、∠COA和∠AOD共5个.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：解答题

    如图，有两部不同型号的手机(分别记为A，B)和与之匹配的2个保护盖(分别记为a，b)散乱地放在桌子上．

    (1)若从手机中随机取一部，再从保护盖中随机取一个，求恰好匹配的概率；

    (2)若从手机和保护盖中随机取两个，用画树状图法或列表法求恰好匹配的概率．

    （1）（2） 【解析】试题分析：（1）由题意可得有Aa，Ab，Ba，Bb四种情况．恰好匹配的有Aa，Bb两种情况，然后直接利用概率公式求解即可求得答案； （2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果以及恰好匹配的情况，再利用概率公式即可求得答案． 试题解析：(1)从手机中随机抽取一个，再从保护盖中随机取一个，有Aa，Ab，Ba，Bb四种结果，每种结果出现的可能性...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：单选题

    一次掷两枚质地均匀的硬币，出现两枚硬币都正面朝上的概率是（ ）

    A. B. C. D.

    D 【解析】试题分析：先利用列表法与树状图法表示所有等可能的结果n，然后找出某事件出现的结果数m，最后计算概率．同时掷两枚质地均匀的硬币一次，共有正正、反反、正反、反正四种等可能的结果，两枚硬币都是正面朝上的占一种，所以两枚硬币都是正面朝上的概率=1÷4=．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：解答题

    如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．

    （1）求证：BG＝CF．

    （2）请你判断BE+CF与EF的大小关系，并说明理由．

    （1）证明见解析；（2）BE+CF＞EF．理由见解析． 【解析】试题分析:（1）先利用ASA判定△BGD≌△CFD，从而得出BG=CF； （2）再利用全等的性质可得GD=FD，再有DE⊥GF，从而得出EG=EF，两边和大于第三边从而得出BE+CF＞EF． 试题解析：（1）∵BG∥AC， ∴∠DBG=∠DCF． ∵D为BC的中点， ∴BD=CD 又∵∠BDG...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：填空题

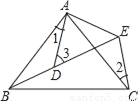
    如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.

    55° 【解析】求出∠BAD=∠EAC，证△BAD≌△EAC，推出∠2=∠ABD=30°，根据三角形的外角性质求出即可． 【解析】 ∵∠BAC=∠DAE， ∴∠BAC﹣∠DAC=∠DAE﹣∠DAC， ∴∠1=∠EAC， 在△BAD和△EAC中， AB=AC，∠BAD=∠EAC， ∴△BAD≌△EAC（SAS）， ∴∠2=∠ABD=30°， ∵...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学人教版上册 全册综合测试卷 题型：单选题

    已知等腰三角形的一边长为5，另一边长为10，则这个等腰三角形的周长为( )

    A. 25 B. 25或20 C. 20 D. 15

    A 【解析】 试题分析：分两种情况： 当腰为5时，5+5=10，所以不能构成三角形； 当腰为10时，5+10＞10，所以能构成三角形，周长是：10+10+5=25cm． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：填空题

    化简： = __________。

    【解析】 = = = .

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：解答题

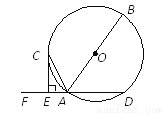
    如图，AB是⊙O的直径，AD是⊙O的弦，点F是DA延长线上的一点，过⊙O上一点C作⊙O的切线交DF于点E，CE⊥DF．

    (1)求证：AC平分∠FAB；

    (2)若AE＝1，CE＝2，求⊙O的半径．

    （1）证明见解析；（2） 【解析】试题分析：（1）连接OC，根据切线的性质和圆周角定理，得出∠OCA=∠OAC与∠CAE=∠OCA，然后根据角平分线的定义可证明； （2）由圆周角定理得到∠BCA=90°，由垂直的定义，可求出∠CEA=90°，从而根据两角对应相等的两三角形相似可证明△ACB∽△AEC，再根据相似三角形的对应边成比例求得AB的长，从而得到圆的半径. 试题解析：(1)...

    查看答案和解析>>

    同步练习册答案