
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是__________.

【答案】(3,4)或(![]() ,4)或(6﹣
,4)或(6﹣![]() ,4)
,4)
【解析】分析:由矩形的性质得出BC=OA=6,AB=OC=4,∠B=∠OCB=90°,分三种情况:①当PO=PA时;②当AP=AO=6时;③当OP=OA=6时;分别求出PC的长,即可得出结果.
详解:∵四边形OABC是矩形,

∴BC=OA=6,AB=OC=4,∠B=∠OCB=90°,
分三种情况:如图所示:
①当PO=PA时,P在OA的垂直平分线上,P是BC的中点,PC=3,
∴点P的坐标为(3,4);
②当AP=AO=6时,BP=![]() ,
,
∴PC=6-2![]() ,
,
∴P(6-2![]() ,4);
,4);
③当OP=OA=6时,PC=![]() ,
,
∴P(2![]() ,4).
,4).
综上所述:点P的坐标为(3,4)或(2![]() ,4)或(6-2
,4)或(6-2![]() ,4).
,4).
故答案为:(3,4)或(2![]() ,4)或(6-2
,4)或(6-2![]() ,4).
,4).


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中(请补画出必要的图形),![]() 为坐标原点,直线y=-2x+4与
为坐标原点,直线y=-2x+4与![]() 、
、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,过线段
两点,过线段![]() 的中点
的中点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,分别与直线
,分别与直线![]() 交于点
交于点![]() ,与直线y=x+n交于点
,与直线y=x+n交于点![]() .
.
(1)直接写出点A、B、C、![]() 的坐标:A(____________),B(____________),C(_____________),D(____________);
的坐标:A(____________),B(____________),C(_____________),D(____________);

(2)若![]() 的面积等于1,求点P的坐标.
的面积等于1,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的变形规律:
![]() ;
;![]() ;
;![]() ;….
;….
解答下面的问题:
(1)仿照上面的格式请写出![]() = ;
= ;
(2)若n为正整数,请你猜想![]() = ;
= ;
(3)基础应用:计算:![]() .
.
(4)拓展应用1:解方程:![]() =2016
=2016
(5)拓展应用2:计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持抗震救灾,我市A、B两地分别有赈灾物资100吨和180吨,需全部运往重灾区C、D两县,根据灾区的情况,这批赈灾物资运往C县的数量比运往D县的数量的2倍少80吨.
(1)求这批赈灾物资运往C、D两县的数量各是多少吨?
(2)设A地运往C县的赈灾物资数量为x吨(x为整数).若要B地运往C县的赈灾物资数量大于A地运往D县赈灾物资数量的2倍,且要求B地运往D县的赈灾物资数量不超过63吨,则A、B两地的赈灾物资运往C、D两县的方案有几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
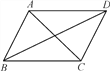
A. 当AB=BC时,它是菱形 B. 当AC=BD时,它是正方形
C. 当∠ABC=90°时,它是矩形 D. 当AC⊥BD时,它是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于 . 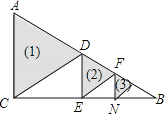
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com