
【题目】以下是某省2010年教育发展情况有关数据:
全省共有各级各类学校25000所,其中小学12500所,初中2000所,高中450所,其它学校10050所;全省共有在校学生995万人,其中小学440万人,初中200万人,高中75万人,其它280万人;全省共有在职教师48万人,其中小学20万人,初中12万人,高中5万人,其它11万人.
请将上述资料中的数据按下列步骤进行统计分析.
(1)整理数据:请设计一个统计表,将以上数据填入表格中.
(2)描述数据:下图是描述全省各级各类学校所数的扇形统计图,请将它补充完整.
(3)分析数据:
①分析统计表中的相关数据,小学、初中、高中三个学段的师生比,最小的是哪个学段?请直接写出.(师生比=在职教师数︰在校学生数)
②根据统计表中的相关数据,你还能从其它角度分析得出什么结论吗?(写出一个即可)
③从扇形统计图中,你得出什么结论?(写出一个即可)

科目:初中数学 来源: 题型:
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:
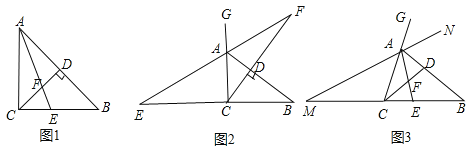
(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.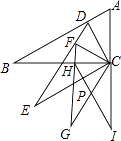
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.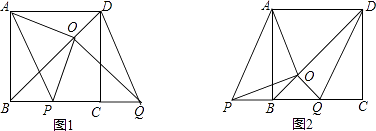
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB , BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30 ![]() m到达A′处,
m到达A′处,
(1)求A,B之间的距离;
(2)求从无人机A′上看目标D的俯角的正切值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD的外接圆上的一动点(点C不在 ![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°
上,且不与点B,D重合),∠ACB=∠ABD=45° 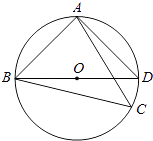
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证: ![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2 , AM2 , BM2三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试找出如图所示的每个正多边形的对称轴的条数,并填入表格中.
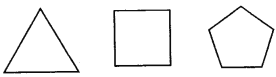
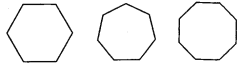
正多边形的边数 | 3 | 4 | 5 | 6 | 7 | 8 |
对称轴的条数 |
根据上表,请就一个正n边形对称轴的条数作一猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣ ![]() [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com