
分析 作AC⊥x轴于C,如图,易得△OAC为等腰直角三角形,则∠AOC=45°,OA=$\sqrt{2}$OC=2$\sqrt{2}$,再根据旋转的性质得点B在x轴的正半轴上,OB=OA=2$\sqrt{2}$,然后根据x轴上点的坐标特征写出B点坐标.
解答 解:作AC⊥x轴于C,如图,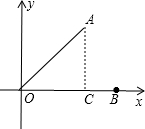
∵点A的坐标为(2,2),
∴OC=AC=2,
∴△OAC为等腰直角三角形,
∴∠AOC=45°,OA=$\sqrt{2}$OC=2$\sqrt{2}$,
∵点A绕原点顺时针旋转45°后得到点B,
∴∠AOB=45°,即点B在x轴的正半轴上,且OB=OA=2$\sqrt{2}$,
∴B点坐标为(2$\sqrt{2}$,0).
故答案为(2$\sqrt{2}$,0).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


科目:初中数学 来源: 题型:解答题
 如图,AB之间是一个湖泊,为了既不破坏湖泊的自然风光,又方便湖对岸的交通往来,现准备在湖底修一条隧道,在A地测得隧道位于北偏东51°方向,如果A、B两地同时开工,那么在B地按什么方向施工,才能使隧道准确接通?请说明理由.
如图,AB之间是一个湖泊,为了既不破坏湖泊的自然风光,又方便湖对岸的交通往来,现准备在湖底修一条隧道,在A地测得隧道位于北偏东51°方向,如果A、B两地同时开工,那么在B地按什么方向施工,才能使隧道准确接通?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 通常温度降到0℃以下,纯净的水会结冰 | |
| B. | 随意翻到一本书的某页,这页的页码是奇数 | |
| C. | 明天的太阳从东方升起 | |
| D. | 在一个不透明的袋子里装有完全相同的6个红色小球,随机抽取一个白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com