
平面直角坐标中,直线OA、OB都经过第一象限(O是坐标原点),且满足∠AOB=45°,如直线OA的解析式为y=kx,现探究直线OB解析式情况。
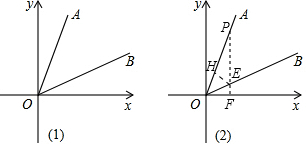
(1) 当∠BOX=30°时(如图1),求直线OB解析式;
(2) 当k=2时(如图2),探究过程:OA上取一点P(1, 2)作PF⊥x轴于F,交OB于E,作EH⊥OA于H,则= ,根据以上探究过程,请求出直线
OB解析式;
(3) 设直线OB解析式为y=mx,则m= (用k表示),如 双曲线交OA于M, 交OB于N,当OM=ON时,求k的值。
科目:初中数学 来源: 题型:
 反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| OH |
| PH |
| 1 |
| 2 |
| 1 |
| 2 |
| k-1 |
| k+1 |
| k+1 |
| 1-k |
| k-1 |
| k+1 |
| k+1 |
| 1-k |
| n |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
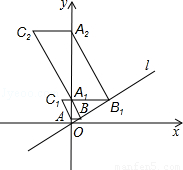
 (2013•铁岭)如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是
(2013•铁岭)如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作![]() ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作
ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作![]() A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(辽宁铁岭卷)数学(解析版) 题型:填空题
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作 ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作
ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作 A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com