Question

20．问题情境：
如图1，在菱形ABCD中，点E、F分别为AB，BC边上的点，连接AF，DE相交于点O，且∠AOE=∠ADC，试探究：AF与DE的数量关系．
特例探究：
如图2，当菱形ABCD是正方形时，AF与DE有怎样的数量关系呢？请你直接写出结论，不必证明；
类比解答：
类比特例探究的结论，猜想问题情境中AF与DE的数量关系，并说明理由；
拓展延伸：
将图1中的菱形ABCD改为?ABCD（如图3）其中AB=a，AD=b，点E、F、G、H分别为AB、BC、CD、DA边上的动点，连接EG、HF相交于点O，且∠HOE=∠ADC，试探究：EG与FH的数量关系，用含a、b的式子直接写出$\frac{EG}{FH}$的值，不必说明理由．

Answer 1

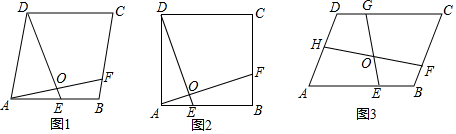
分析 （1）特例探究：根据四边形ABCD是正方形，以及∠AOE=∠ADC可得∠ADE=∠BAF，即可判定△ADE≌△BAF（ASA），进而得出AF=DE；
（2）类比解答：在AB上取点M使得DM=DA，连接DM，交AF于N，再判定△ABF≌△DME，即可得出AF=DE；
（3）拓展延伸：过G作GM⊥AB于M，过H作HN⊥BC于N，根据平行四边形面积公式，求出$\frac{GM}{HN}$=$\frac{b}{a}$，再根据∠GME=∠HNF=90°，∠GEM=∠HFN，证出△GME∽△HNF即可得出$\frac{EG}{FH}$的值．

解答 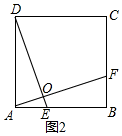解：（1）特例探究：AF=DE．
理由：如图2，∵四边形ABCD是正方形，
∴AD=BA，∠DAE=∠B=90°，
∵∠AOE=∠ADC=90°，
∴∠ADE+∠DAO=∠BAF+∠DAO=90°，
∴∠ADE=∠BAF，
∴在ADE和△BAF中，
$\left\{\begin{array}{l}{∠ADE=∠BAF}\\{AD=BA}\\{∠DAE=∠B}\end{array}\right.$，
∴△ADE≌△BAF（ASA），
∴AF=DE；

（2）类比解答：AF与DE的数量关系为AF=DE．
理由：如图1，在AB上取点M使得DM=DA，连接DM，交AF于N，则
∠DAM=∠DMA，DM=AD=AB，
∵∠DAB+∠B=180°，∠DMA+∠DME=180°，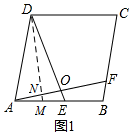
∴∠DME=∠B，
∵∠AOE=∠ADC，
∴∠ADO+∠DAO=∠ADO+∠CDO，
∴∠DAO=∠CDO，
又∵CD∥AB，AD∥BC，
∴∠CDO=∠MED，∠DAO=∠BFA，
∴∠MED=∠BFA，
在△MED和△BFA中，
$\left\{\begin{array}{l}{∠DME=∠B}\\{∠MED=∠BFA}\\{DM=AB}\end{array}\right.$，
∴△MED≌△BFA（AAS），
∴AF=DE；

（3）拓展延伸：$\frac{EG}{FH}$=$\frac{b}{a}$．
如图3，过G作GM⊥AB于M，过H作HN⊥BC于N，
∵四边形ABCD是平行四边形，
∴AD∥BC，DC∥AB，
∵平行四边形ABCD的面积=AB×GM=BC×HN，
∵AB=a，AD=b，
∴$\frac{GM}{HN}$=$\frac{b}{a}$，
∵GM⊥AB，HN⊥BC，
∴∠GME=∠HNF=90°，
∵∠ADC=∠HOE，
∴∠ADC+∠HOG=∠EOH+∠HOG=180°，
∴∠DHO+∠DGE=360°-180°=180°，
∵AD∥BC，DC∥AB，
∴∠NFH=∠DHF，∠DGE+∠GEM=180°，
∴∠HFN=∠GEM，
∴△GME∽△HNF，
∴$\frac{EG}{FH}$=$\frac{GM}{HN}$=$\frac{b}{a}$．

点评 本题属于四边形综合题，主要考查了正方形的性质，平行四边形的性质，菱形的性质，面积公式，全等三角形的性质和判定，相似三角形的性质和判定的综合应用，解决问题的关键是作辅助线构造全等三角形或相似三角形，依据全等三角形的对应边相等或相似三角形的对应边成比例得出结论．