
| A. | 29 | B. | 21或29 | C. | 21或22 | D. | 21、22或29 |
分析 在等腰梯形ABCD中,AD∥BC,AB=CD,作AE∥CD,则四边形AECD是平行四边形,△ABE是等腰三角形,分三种情形讨论,根据三角形三边关系定理判断是否存在.
解答 解:如图,在等腰梯形ABCD中,AD∥BC,AB=CD,作AE∥CD,则四边形AECD是平行四边形,△ABE是等腰三角形,
①若AB=CD=3,AD=4,BC=11,则在△ABE中,AB=AE=3,BE=7,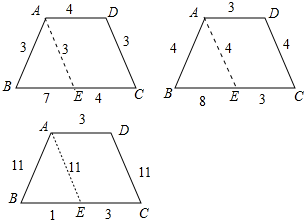
∵3+3<7,
∴△ABE不存在,此种等腰梯形不存在.
②若AB=CD=4,AD=3,BC=11,则在△ABE中,AB=AE=4,BE=8,
∵4+4=8,
∴△ABE不存在,此种等腰梯形不存在.
③若AB=CD=11,AD=3,BC=4,则在△ABE中,AB=AE=11,BE=1,
∵11+11>1,
∴△ABE存在,
此时等腰梯形的周长为3+11+11+4=29.
故选A.
点评 本题考查等腰梯形的性质、三角形三边关系定理等知识,解题的关键是学会添加常用辅助线,把四边形问题转化为三角形问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若x+y=0,则点P(x,y)一定在第二、四象限角平分线上 | |
| B. | 在x轴上的点纵坐标为0 | |
| C. | 点P(-1,3)到y轴的距离是1 | |
| D. | 点A(-a2-1,|b|)一定在第二象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
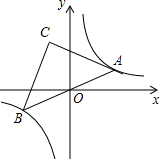 如图,点A是双曲线y=$\frac{4}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{4}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=-$\frac{1}{4}$x | B. | y=-$\frac{1}{2}$x | C. | y=-$\frac{4}{x}$ | D. | y=-$\frac{2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ab-b=b(a-b) | B. | x2-(-2)2=(x+2)(x-2) | C. | m2+4m+4=m2+4(m+1) | D. | x2-x-$\frac{1}{4}$=(x-$\frac{1}{2}$)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把△ABC沿AB平移到△A′B′C′的位置,它们的重叠部分的面积是△ABC面积的一半,若AB=$\sqrt{2}$,求此三角形移动的距离A′A.
如图,把△ABC沿AB平移到△A′B′C′的位置,它们的重叠部分的面积是△ABC面积的一半,若AB=$\sqrt{2}$,求此三角形移动的距离A′A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x-1 | B. | y=-x+1 | C. | y=x+1 | D. | y=-x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com