
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使![]() ,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为______度;
(2)在(1)旋转过程中,当旋转至图3的位置时,使得OM在∠BOC的内部,ON落在直线AB下方,试探究∠COM与∠BON之间满足什么等量关系,并说明理由.

科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() .若将
.若将![]() 绕点
绕点![]() 顺时针旋转至Δ
顺时针旋转至Δ![]() ,使射线
,使射线![]() 与射线
与射线![]() 相交于点
相交于点![]() (不与
(不与![]() 、
、![]() 重合).
重合).
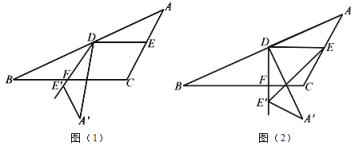
(1)如图(1),若![]() ,则
,则![]() ;
;
(2)如图(2),连结![]() ,若
,若![]() ,试求出
,试求出![]() 的度数;
的度数;
(3)请探究![]() 与
与![]() 之间所满足的数量关系,并加以证明.
之间所满足的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.求证:∠1=∠2.

证明:∵∠AED=∠C(已知),
∴ ∥ ( ),
∴∠B+∠BDE=180°( ),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴ ∥ ( ),
∴ ∠1=∠2( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB= ![]() .
.
(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:问题:某班在购买啦啦操比赛的物资时,准备购买红色、黄色,蓝色三种颜色的啦啦球,其颜色不同则价格不同,第一次买了15个红色啦啦球、7个黄色啦啦球、11个蓝色啦啦球共用1084元,第二次买了2个红色啦啦球、4个黄色啦啦球、3个蓝色啦啦球共用304元,试问第三次买了红、黄、蓝啦啦球各一个共需多少元?(假定三次购买红、黄、蓝啦啦球单价不变)
解:设购买红、黄、蓝啦啦球的单价分别为x、y、z元,依题意得:
![]()
上述方程组可变形为:![]()
设x+y+z=m,2x+z=n,上述方程组又可化为:![]()
①+4×②得:m= ,即x+y+z= ;
答:第三次购买红、黄、蓝啦啦球各一个共需 元.
阅读后,细心的你,可以解决下列问题:
某同学买13支黑笔、5支红笔、9个笔记本,共用去92.5元:如果买2支黑笔、4支红笔、3个笔记本,则共用去32元,试问只买一支黑笔、一支红笔、一个笔记本,共需多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.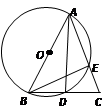
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD、CD.
(1)求证:AD=CD;
(2)①画图:在AC边上找一点H,使得BH+EH最小(要求:写出作图过程并画出图形,不用说明作图依据);
②当BC=2时,求出BH+EH的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com