
 ��ͼ��һ�κ���y=-$\frac{{\sqrt{3}}}{3}$x+1��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ�������ȱߡ�ABC��
��ͼ��һ�κ���y=-$\frac{{\sqrt{3}}}{3}$x+1��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ�������ȱߡ�ABC������ ��1����ֱ�߽���ʽ�����A��B���꣬��Rt��AOB�У��������Ǻ����������á�BAO=30�㣬�ҿ����AB�ij����Ӷ������CA��OA��������C�����꣬���ô���ϵ��������÷�������������ʽ��
��2���֡�PAD�ס�ABO�͡�PAD�ס�BAO����������ֱ��������������ε����ʿ����m��ֵ�������P�����꣬���뷴������������ʽ������֤���ɣ�
��� �⣺
��1����y=-$\frac{{\sqrt{3}}}{3}$x+1�У���y=0�ɽ��x=$\sqrt{3}$����x=0�ɵ�y=1��
��A��$\sqrt{3}$��0����B��0��1����
��tan��BAO=$\frac{OB}{OA}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$��
���BAO=30�㣬
�ߡ�ABC�ǵȱ������Σ�
���BAC=60�㣬
���CAO=90�㣬
��Rt��BOA�У��ɹ��ɶ����ɵ�AB=2��
��AC=2��
��C��$\sqrt{3}$��2����
�ߵ�C�ڷ���������y=$\frac{k}{x}$��ͼ���ϣ�
��k=2��$\sqrt{3}$=2$\sqrt{3}$��
�෴������������ʽΪy=$\frac{2\sqrt{3}}{x}$��
��2����P��2$\sqrt{3}$��m���ڵ�һ���ޣ�
��AD=OD-OA=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$��PD=m��
����ADP�ס�AOBʱ������$\frac{PD}{OB}$=$\frac{AD}{OA}$����$\frac{m}{1}$=$\frac{\sqrt{3}}{\sqrt{3}}$�����m=1����ʱP������Ϊ��2$\sqrt{3}$��1����
����PDA�ס�AOBʱ������$\frac{PD}{OA}$=$\frac{AD}{OB}$����$\frac{m}{\sqrt{3}}$=$\frac{\sqrt{3}}{1}$�����m=3����ʱP������Ϊ��2$\sqrt{3}$��3����
��P��2$\sqrt{3}$��3������y=$\frac{2\sqrt{3}}{x}$�ɵ�3��$\frac{2\sqrt{3}}{2\sqrt{3}}$��
��P��2$\sqrt{3}$��3�����ڷ���������ͼ���ϣ�
��P��2$\sqrt{3}$��1�����뷴������������ʽ��1=$\frac{2\sqrt{3}}{2\sqrt{3}}$��
��P��2$\sqrt{3}$��1���ڷ���������ͼ���ϣ�
���Ͽ�֪P������Ϊ��2$\sqrt{3}$��1����
���� ����Ϊ�������������ۺ�Ӧ�ã��漰����ϵ�������ȱ������ε����ʡ����Ǻ��������ɶ��������������ε����ʼ���������˼���֪ʶ���ڣ�1�������C�������ǽ���Ĺؼ����ڣ�2�����������������ε����ʵõ�m�ķ����ǽ���Ĺؼ���ע���������������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
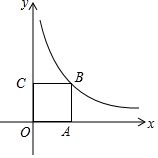 ��ͼ����B�ڷ���������y=$\frac{4}{x}$��x��0����ͼ���ϣ���A��C�ֱ���x�ᡢy���������ϣ����ı���OABCΪ�����Σ�
��ͼ����B�ڷ���������y=$\frac{4}{x}$��x��0����ͼ���ϣ���A��C�ֱ���x�ᡢy���������ϣ����ı���OABCΪ�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У�ƽ���ı���OABC�Ķ���A������Ϊ��-4��0��������B�ڵڶ����ޣ���BAO=60�㣬BC��y���ڵ�D��DB��DC=3��1��������y=$\frac{k}{x}$��k��0��x��0����ͼ����C����k��ֵΪ��������
��ͼ����ƽ��ֱ������ϵ�У�ƽ���ı���OABC�Ķ���A������Ϊ��-4��0��������B�ڵڶ����ޣ���BAO=60�㣬BC��y���ڵ�D��DB��DC=3��1��������y=$\frac{k}{x}$��k��0��x��0����ͼ����C����k��ֵΪ��������| A�� | $\frac{{\sqrt{3}}}{3}$ | B�� | $\frac{{\sqrt{3}}}{2}$ | C�� | $\frac{{2\sqrt{3}}}{3}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
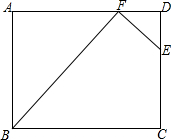 ��ͼ��ABCD�dz����Σ�AB=6��BC=8��CE=4���ı���BCEF�������30����ô������DEF������Ƕ��٣�
��ͼ��ABCD�dz����Σ�AB=6��BC=8��CE=4���ı���BCEF�������30����ô������DEF������Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 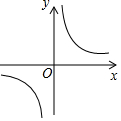 | C�� | 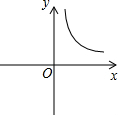 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С������ѧϰ�����ľ��飬�Ժ���y=$\frac{4}{{��x-1��}^{2}+1}$��ͼ�������ʽ�����̽����������С����̽�����̣��벹�������������������⣺
С������ѧϰ�����ľ��飬�Ժ���y=$\frac{4}{{��x-1��}^{2}+1}$��ͼ�������ʽ�����̽����������С����̽�����̣��벹�������������������⣺| x | �� | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | �� |
| y | �� | $\frac{2}{5}$ | $\frac{4}{5}$ | $\frac{16}{13}$ | 2 | $\frac{16}{5}$ | 4 | $\frac{16}{5}$ | 2 | $\frac{16}{13}$ | $\frac{4}{3}$ | m | �� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com