
如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部份)为s,s关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积;
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
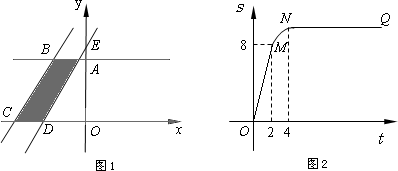
|
解:
(1)① ②当 直角梯形OABC被直线
(2)存在………………………………………1分 对于第(2)题我们提供如下详细解答(评分无此要求).下面提供参考解法二: 以点D为直角顶点,作
E点在0点与A点之间不可能; ②以点E为直角顶点
同理在②二图中分别可得 以点P为直角顶点
同理在③二图中分别可得 综上可得 下面提供参考解法二: 以直角进行分类进行讨论(分三类): 第一类如上解法(1)中所示图 第二类如上解法②中所示图
综上可得 事实上,我们可以得到更一般的结论: 如果得出
|


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》常考题集(23):2.8 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》常考题集(22):20.5 二次函数的一些应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷36(义桥实验学校 严炯炯)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com