
【题目】如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(1)①∠BCE与∠CDF的大小关系是_______________;
②证明:GF⊥BF;
(2)探究G落在边DC的什么位置时,BF=BC,请说明理由.

【答案】 (1)①∠BCE=∠CDF②见解析;(2) 当G落在线段DC的中点时,BF=BC,理由见解析.
【解析】分析:
(1)①由DF⊥CE可得∠DFC=90°,从而可得∠CDF+∠DCF=90°,结合∠DCF+∠BCE=90°可得∠BCE=∠CDF;
②由已知条件易证△DEF∽△CDF,从而可得![]() ,结合①中所得∠BCE=∠CDF可得△DGF∽△BCF,由此可得∠DFG=∠BFC,结合∠DFG+∠GFC =90度可得∠BFC+∠GFC=90°,由此可得∠GFB=90°,从而可得GF⊥BF;
,结合①中所得∠BCE=∠CDF可得△DGF∽△BCF,由此可得∠DFG=∠BFC,结合∠DFG+∠GFC =90度可得∠BFC+∠GFC=90°,由此可得∠GFB=90°,从而可得GF⊥BF;
(2)连接BG,若BF=BC,则由(1)中所得∠GFB=90°结合∠BCG=90°,易得△BFG≌△BCG,由此可得GF=GC,在Rt△DFC中,再证GF=GD,即可得到此时点G是CD的中点,由此可知,当点G是CD的中点时,BF=BG.
详解:
(1)①∠BCE=∠CDF
②∵四边形ABCD为正方形
∴CD⊥AD,CB=CD
∵DF⊥CE
∴△DEF∽△CDF
∴![]()
又∵DE=DG,BC=CD
∴![]()
由①知∠BCE=∠CDF
∴△DGF∽△BCF
∴∠DFG=∠BFC
∴∠DFG+∠GFC =∠BFC+∠GFC
即∠GFB=∠DFC=900
∴GF⊥BF
(2)当G落在线段DC的中点时,BF=BC,理由如下:
连接BG,由已知和以上结论知,△BFG和△BCG都是直角三角形,

若BF=BC,又BG=BG
∴Rt△BFG≌Rt△BCG
∴CG=FG
又∵△DFC为直角三角形
∴G为DC的中点.
故当G落在线段DC的中点时,BF=BC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某工厂接受了 20 天内生产1200 台GH 型电子产品的总任务。已知每台GH 型产品由 4 个G 型装 置和3 个 H 型装置配套组成。工厂现有80 名工人,每个工人每天能加工6 个G 型装置或3 个 H 型装置。工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G 、H 型装置数量正好组成GH 型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH 型电子产品?
(2)工厂补充 40名新工人,这些新工人只能独立进行G 型装置的加工,且每人每天只能加工 4个G型装置,则补充新工人后每天能配套生产多少产品?补充新工人后20天内能完成总任务吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BA=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
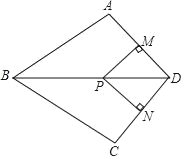
(1)求证:点A与C关于直线BD对称.
(2)若∠ADC=90°,求证四边形MPND为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE∥BF,CE=BF.则添加下列条件还不能使△EAC≌△FDB.( )

A. AB=CDB. AE∥DFC. ∠E=∠FD. AE=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)
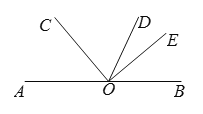
解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() 给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,
给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,![]() ),(2,
),(2,![]() ),都是“同心有理数对”.
),都是“同心有理数对”.
(1)数对(﹣2,1),(3,![]() )是 “同心有理数对”的是__________.
)是 “同心有理数对”的是__________.
(2)若(a,3)是“同心有理数对”,求a的值;
(3)若(m,n)是“同心有理数对”,则(﹣n,﹣m) “同心有理数对”(填“是”或“不是”),说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A,B,C是数轴上的三个点,其中AB=12,且A,B两点表示的数互为相反数.
![]()
(1)请在数轴上标出原点O,并写出点A表示的数;
(2)如果点Q以每秒2个单位的速度从点B出发向左运动,那么经过 秒时,点C恰好是BQ的中点;
(3)如果点P以每秒1个单位的速度从点A出发向右运动,那么经过多少秒时PC=2PB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某县为创建省文明卫生城市,计划将城市道路两旁的人行道进行改造,经调查可知,若该工程由甲工程队单独来做恰好在规定时间内完成;若该工程由乙工程队单独完成,则需要的天数是规定时间的2倍,若甲、乙两工程队合作6天后,余下的工程由甲工程队单独来做还需3天完成.
(1)问该县要求完成这项工程规定的时间是多少天?
(2)已知甲工程队做一天需付给工资5万元,乙工程队做一天需付给工资3万元.现该工程由甲、乙两个工程队合作完成,该县准备了工程工资款65万元.请问该县准备的工程工资款是否够用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com