
| A. | $\left\{\begin{array}{l}{x+y=34}\\{x+1=2y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=34}\\{x=2y+1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=34}\\{2x=y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+2y=34}\\{x=2y+1}\end{array}\right.$ |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
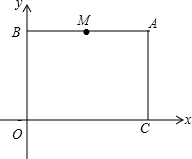 平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C.M是线段AB的中点,点P从M点出发沿线段MA-AC向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t(秒).
平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C.M是线段AB的中点,点P从M点出发沿线段MA-AC向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在索契冬奥会中,中国体育代表团取得了3金、4银、2铜的好成绩,某校为了解同学对短道速滑、滑雪、花样滑冰三个项目的喜爱情况,随机抽取了一定数量的同学进行调查,得到如下统计图表.
在索契冬奥会中,中国体育代表团取得了3金、4银、2铜的好成绩,某校为了解同学对短道速滑、滑雪、花样滑冰三个项目的喜爱情况,随机抽取了一定数量的同学进行调查,得到如下统计图表.| 项目 | 短道速滑 | 滑雪 | 花样滑冰 |
| 频数 | 25 | a | 10 |
| 频率 | 50% | 30% | b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
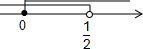 一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )| A. | 0<x≤$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | 0≤x<$\frac{1}{2}$ | D. | x>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com